早教吧作业答案频道 -->数学-->
如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE,过A点向BC作垂线AG.反向延长AG交DE于H.(1)求证:S△ADE=S△ABC;(2)求证:AG平分DE.
题目详情
如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE,过A点向BC作垂线AG.反向延长AG交DE于H.
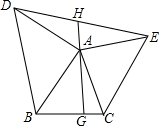
(1)求证:S△ADE=S△ABC;
(2)求证:AG平分DE.

(1)求证:S△ADE=S△ABC;
(2)求证:AG平分DE.
▼优质解答
答案和解析
(1)证明:作DP⊥GA,EQ⊥GA,垂足分别为P、Q.
∵Rt△ABD是等腰三角形,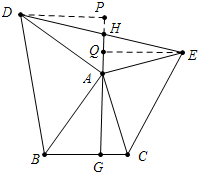
∴DA=BA,
∵∠PDA+∠PAD=90°,
∠PAD+∠BAG=90°,
∴∠PDA=∠BAG,
在△DAP与△ABG中,
,
∴△DAP≌△ABG(AAS),
∴DP=AG,
同理△AGC≌△EQA,AG=FQ.,
∴DP=EQ,
∴S△ABG=S△DAP,S△EQA=S△AGC,
在△DPH与△EQH中,
,
∴△DPH≌△EQH(AAS),
∴S△DPH=S△EQH,
∴S△ABC=S△ABG+S△AGC=S△DAP-S△DPH+S△EQA-S△EQH=S△DAP+S△EQA=S△ADE,
即S△ABC=S△ADE.
(2)证明:∵△DPH≌△EQH(已证),
∴DH=HE,
∴AG平分DE.
∵Rt△ABD是等腰三角形,

∴DA=BA,
∵∠PDA+∠PAD=90°,
∠PAD+∠BAG=90°,
∴∠PDA=∠BAG,
在△DAP与△ABG中,
|
∴△DAP≌△ABG(AAS),
∴DP=AG,
同理△AGC≌△EQA,AG=FQ.,
∴DP=EQ,
∴S△ABG=S△DAP,S△EQA=S△AGC,
在△DPH与△EQH中,
|
∴△DPH≌△EQH(AAS),
∴S△DPH=S△EQH,
∴S△ABC=S△ABG+S△AGC=S△DAP-S△DPH+S△EQA-S△EQH=S△DAP+S△EQA=S△ADE,
即S△ABC=S△ADE.
(2)证明:∵△DPH≌△EQH(已证),
∴DH=HE,
∴AG平分DE.
看了 如图,在△ABC中,以A为顶...的网友还看了以下:
提示:D-C=0A-B,A-D,D-C,D-E,E-F=1A-D,C-F=2A-B,D-E,E-F 2020-04-06 …
已知A与(B或C)=D,能否得出结论:Aand非(B与C)=非D?已知定理:A与(B或C)=D如: 2020-04-06 …
把下面的式子写成(A+B)(A-B)的形式(1)(a+b+c+d)(-a-b+c+d)(2)(把下 2020-04-27 …
24 (a+b)/(c+d)=(√a^2+b^2)/√ (c^2+d^2)成立证明:(1)a/b= 2020-05-14 …
若非空集合M⊆N={a,b,c,d},则M的个数为8个{a},{b},{c},{d},{a,b}, 2020-05-15 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
如果正数a,b,c,d满足a+b=cd=4,那么()A.ab≤c+d且等号成立时a,b,c,d的取 2020-07-09 …
区间(c,d),[c,d],(c,d],[c,d)的长度均为d-c,已知a大于b,则求1/(x-a 2020-07-25 …
WPS表格敢不敢有这种公式A,B,C,D四个格子,A-B=C,D为公式lF(B<25且C>=0WPS 2020-11-29 …
设C,D是两个随机事件,下面哪个叙述是正确的()A.C∩D与C∪D互斥B.C∩D与C∩(D的对立事件 2020-12-01 …