早教吧作业答案频道 -->数学-->
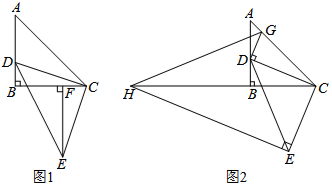
△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;(2)在图1中,连接AE交BC于M,求ADBM
题目详情
△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求
的值;
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH,当点D在边AB上运动时,探究线段HE,HG与DG之间的数量关系,并证明你的结伦.
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求
| AD |
| BM |
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH,当点D在边AB上运动时,探究线段HE,HG与DG之间的数量关系,并证明你的结伦.

▼优质解答
答案和解析
 (1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
(1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
∴CD=CE,∠DCB+∠ECF=90°,
∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中,
,
∴△DBC≌△CFE;
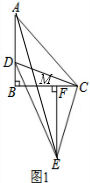
(2) 如图1,
∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中,
,
∴△ABM≌△EFM,
∴BM=FM,
∴BF=2BM,
∴AD=2BM,
∴
的值为2;
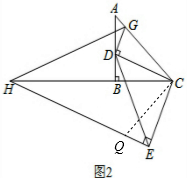 (3) HE=GH+GD,
(3) HE=GH+GD,
在EH上截取EQ=DG,如图2,
在△CDG和△CEQ中
,
∴△CDG≌△CEQ,
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中,
,
∴△HCG≌△HCQ,
∴HG=HQ,
∴HE=HQ+QE=HG+DG.
 (1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
(1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.∴CD=CE,∠DCB+∠ECF=90°,
∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中,
|
∴△DBC≌△CFE;
(2) 如图1,
∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中,
|
∴△ABM≌△EFM,
∴BM=FM,
∴BF=2BM,
∴AD=2BM,
∴
| AD |
| BM |
 (3) HE=GH+GD,
(3) HE=GH+GD,在EH上截取EQ=DG,如图2,
在△CDG和△CEQ中
|
∴△CDG≌△CEQ,
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中,
|
∴△HCG≌△HCQ,
∴HG=HQ,
∴HE=HQ+QE=HG+DG.
看了 △ABC为等腰直角三角形,∠...的网友还看了以下:
八年级下册人教版物理第七章力下列关于力的说法中,错误的是()A力是物体对物体的作用B只有相互接触的 2020-05-13 …
对包含n个元素的散列表进行检索,平均检索长度为( )。A.O(log2n)B.O(n)C.O(n*l 2020-05-23 …
对包含n个元素的散列表进行检索,平均检索长度( )。A.为O(log2n)B.为O(n)C.为O(n 2020-05-23 …
对包含n个元素的散列表进行检索,平均检索长度A.为O(10g2n)B.为O(n)C.为O(nlog2 2020-05-23 …
对含有n个元素的散列表进行检索,平均检索长度为______。A.O(n2)B.O(nlog2n)C. 2020-05-24 …
对包含n个元素的散列表进行检索,平均检索长度A.为O(log2n)B.为O(n)C.为O(n*log 2020-05-24 …
对包含n个元素的散列表进行检索,平均检索长度为A.为O(log2n)B.为O(n)C.为O(n*lo 2020-05-24 …
秦代官吏在审判时量刑不当为()。A.诬人罪B.不审罪C.失刑罪D.不直罪 2020-06-04 …
我国煤矿井下使用的变压器中性点采用( )方式。A.通过补偿电阻接地B.直接接地C.与地无关D.不直接 2020-06-07 …
坐一会站起来腰挺不直 2021-06-11 …