早教吧作业答案频道 -->数学-->
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.(1)求证:DF=DE;(2)连接EF,若BE=8,CF=6,求△DEF的面积.
题目详情
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
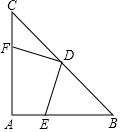
(1)求证:DF=DE;
(2)连接EF,若BE=8,CF=6,求△DEF的面积.

(1)求证:DF=DE;
(2)连接EF,若BE=8,CF=6,求△DEF的面积.
▼优质解答
答案和解析
(1)证明:连接AD.
∵AB=AC,D为BC的中点,
∴AD⊥BC,
又∵∠BAC=90°,
∴AD=CD=BD,∠C=∠DAE=45°,
∵DE⊥DF,
∴∠CDF+∠ADF=∠ADE+∠ADF,
∴∠CDF=∠ADE,
在△CDF和△ADE中
,
∴△CDF≌△ADE(ASA),
∴DF=DE.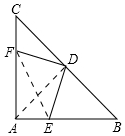
(2)连接EF.由(1)知,AE=CF=6,同理AF=BE=8
∵∠EAF=90°
∴EF=
=
=10,
∵DE=DF,DE⊥DF
∴△DEF为等腰三角形
∴DE2+DF2=EF2=100
∴DE=DF=5
,
∴S△DEF=
•(5
)2=25.
∵AB=AC,D为BC的中点,
∴AD⊥BC,
又∵∠BAC=90°,
∴AD=CD=BD,∠C=∠DAE=45°,
∵DE⊥DF,
∴∠CDF+∠ADF=∠ADE+∠ADF,
∴∠CDF=∠ADE,
在△CDF和△ADE中
|
∴△CDF≌△ADE(ASA),
∴DF=DE.

(2)连接EF.由(1)知,AE=CF=6,同理AF=BE=8
∵∠EAF=90°
∴EF=
| AE2+AF2 |
| 62+82 |
∵DE=DF,DE⊥DF
∴△DEF为等腰三角形
∴DE2+DF2=EF2=100
∴DE=DF=5
| 2 |
∴S△DEF=
| 1 |
| 2 |
| 2 |
看了 如图,在等腰直角三角形ABC...的网友还看了以下:
求老师解答:当一个四边形两组对边当一个四边形两组对边分别平行时,那么它一定是[]A.正方形B.长方 2020-06-13 …
如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.(1)求证:四边形BCDE位似于四边形B 2020-06-13 …
如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A、D在 2020-06-14 …
在线段AB上顺次取三点C、D、E.(1)若C、D、E是AB的四个等分点,画出图形,并求图中所有线段 2020-06-17 …
若限于用同一种正多边形磁砖镶嵌(要求镶嵌的正多边形的边必须与另一正多边形的边重合),则不能镶嵌成一 2020-07-01 …
如图,四边形ABCD是菱形,点D的坐标是(0,3),以点C为顶点的抛物线y=ax2+bx+c恰经过 2020-07-20 …
在线求指导:平面凸多边形各内角成平面凸多边形各内角成等差,最小角内为45°,公差为30°,则此多边 2020-07-25 …
,此抛物线的顶点为D.(1)求此抛物线的解析式;(2)把△ABC绕AB的中点M旋转180°,得到四边 2020-10-30 …
如图,在平面直角坐标系中描出4个点A(0,2),B(-1,0),C(1,-1),D(3,1).(1) 2020-11-10 …
如图所示,回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形盒.两盒 2020-12-09 …