早教吧作业答案频道 -->数学-->
如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).(1)求△ABC的面积;(2)点D为y轴负半轴上一动点,连接BD交x轴于点E,是否存在点D使得S△ADE=S△BCE?若存在,请求
题目详情
如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).
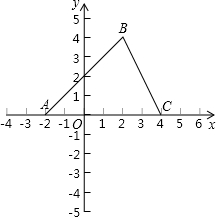
(1)求△ABC的面积;
(2)点D为y轴负半轴上一动点,连接BD交x轴于点E,是否存在点D使得S△ADE=S△BCE?若存在,请求出点D的坐标;若不存在,请说明理由;
(3)若点A、B、C为平行四边形的三个顶点,试写出第四个顶点P的坐标,你的答案唯一吗?
(4)求出(3)中平行四边形的面积.

(1)求△ABC的面积;
(2)点D为y轴负半轴上一动点,连接BD交x轴于点E,是否存在点D使得S△ADE=S△BCE?若存在,请求出点D的坐标;若不存在,请说明理由;
(3)若点A、B、C为平行四边形的三个顶点,试写出第四个顶点P的坐标,你的答案唯一吗?
(4)求出(3)中平行四边形的面积.
▼优质解答
答案和解析
(1)如图1,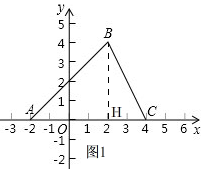 过点B作BH⊥AC于D,
过点B作BH⊥AC于D,
∵A(-2,0),B(2,4),C(4,0),
∴AC=6,BH=4,
∴S△ABC=
AC×BH=
×6×4=12,
(2)如图2,设D(0,b),
∵B(2,4),
∴直线BD的解析式为y=
x+b,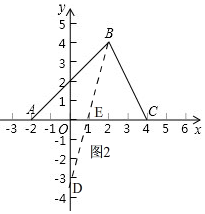
∴E(
,0),
∴AE=
+2,CE=4-
,
∴S△ADE=
AE×OD=
(
+2)×(-b),
S△BCE=
CE×|yB|=
(4-
)×4,
∵S△ADE=S△BCE,
∴
(
+2)×(-b)=
(4-
)×4,
∴b=4(舍)或b=-4,
∴D(0,-4);
(3)答案不唯一,
理由:如图3,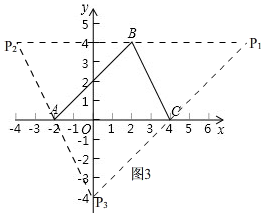
Ⅰ、以AC为边时,过点B作BP1∥AC,
∵B(2,4),
∴直线BP1的解析式为y=4,
∵BP1∥AC,BP1=BP2=AC=6,
∴P1(8,4),P2(-4,4),
Ⅱ、当AC为对角线时,BP3与AC互相平分,
设P3(m,n),
∴m+2=2,n+4=0,
∴m=0,n=-4,
∴P3(0,-4),
即:满足条件的点P(-4,4),(0,-4),(8,4);
(4)由平行四边形的性质得,S平行四边形=2S△ABC=24.
 过点B作BH⊥AC于D,
过点B作BH⊥AC于D,∵A(-2,0),B(2,4),C(4,0),
∴AC=6,BH=4,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图2,设D(0,b),
∵B(2,4),
∴直线BD的解析式为y=
| 4-b |
| 2 |

∴E(
| 2b |
| b-4 |
∴AE=
| 2b |
| b-4 |
| 2b |
| b-4 |
∴S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2b |
| b-4 |
S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2b |
| b-4 |
∵S△ADE=S△BCE,
∴
| 1 |
| 2 |
| 2b |
| b-4 |
| 1 |
| 2 |
| 2b |
| b-4 |
∴b=4(舍)或b=-4,
∴D(0,-4);
(3)答案不唯一,
理由:如图3,

Ⅰ、以AC为边时,过点B作BP1∥AC,
∵B(2,4),
∴直线BP1的解析式为y=4,
∵BP1∥AC,BP1=BP2=AC=6,
∴P1(8,4),P2(-4,4),
Ⅱ、当AC为对角线时,BP3与AC互相平分,
设P3(m,n),
∴m+2=2,n+4=0,
∴m=0,n=-4,
∴P3(0,-4),
即:满足条件的点P(-4,4),(0,-4),(8,4);
(4)由平行四边形的性质得,S平行四边形=2S△ABC=24.
看了 如图,在直角坐标系中,△AB...的网友还看了以下:
初二数学:E(-4,2)F(-1,1),以原点0为位似中心,按比例尺1:2把△EFO缩小,点E的对 2020-05-13 …
在菱形ABCD中,AB=4,角BAD=120°,以A为顶点的△AEF为正三角形.且E在BC上,F在 2020-05-15 …
如图,椭圆E:x^2/100+y^2/25=1的上顶点为A,直线y=-4交椭圆E于点B,C(点B在 2020-05-16 …
求极限lim[cosx-e^(-x^2/2)]/x^4 其中x趋向于0.我的做法为什么错了:lim 2020-05-16 …
设a为常数,并设lim(x->0-)[(4+e^1/x)/(1+e^4/x)]+asinx/|x| 2020-05-17 …
在平面直角坐标系xoy中,已知A(0,b),圆C的半径为1,圆心在直线l:y=2x-4上.1.若在 2020-06-14 …
如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(-4,0),D(0,4) 2020-07-31 …
E(-4,2)F(-1,1),以原点0为位似中心,按比例尺1:2把△EFO缩小,点E的对应点E`的 2020-08-02 …
确定ABC的值,使e^x(1+Bx+Cx^2)=1+Ax+0(x^3)答案A=1/2,B=0,C=- 2020-10-31 …
求证e^i(4π/n)+e^i(8π/n)+...+e^i4(n-1)π/n+e^i(4nπ/n)= 2020-11-01 …