早教吧作业答案频道 -->数学-->
在公差不为0的等差数列{an}中,a1,a4,a8成等比数列.(1)已知数列{an}的前10项和为45,求数列{an}的通项公式;(2)若,且数列{bn}的前n项和为Tn,若,求数列{an}的公
题目详情
在公差不为0的等差数列{a n }中,a 1 ,a 4 ,a 8 成等比数列.
(1)已知数列{a n }的前10项和为45,求数列{a n }的通项公式;
(2)若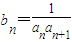 ,且数列{b n }的前n项和为T n ,若
,且数列{b n }的前n项和为T n ,若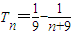 ,求数列{a n }的公差.
,求数列{a n }的公差.
(1)已知数列{a n }的前10项和为45,求数列{a n }的通项公式;
(2)若
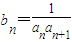 ,且数列{b n }的前n项和为T n ,若
,且数列{b n }的前n项和为T n ,若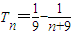 ,求数列{a n }的公差.
,求数列{a n }的公差.▼优质解答
答案和解析
分析:
(1)设等差数列{an}的公差为d,由a1,a4,a8成等比数列得到首项和公差的关系,再由数列{an}的前10项和为45列式求出首项和公差,则答案可求;(2)利用裂项相消法求出数列{bn}的前n项和为Tn,由可求出数列{an}的公差.
设等差数列{an}的公差为d,由a1,a4,a8成等比数列可得,.即,∴,而d≠0,∴a1=9d.(1)由数列{an}的前10项和为45,得,即90d+45d=45,故d=,a1=3,故数列{an}的通项公式为;(2),则数列{bn}的前n项和为Tn===.故数列{an}的公差d=1或d=-1.
点评:
本题考查了等差数列的通项公式,考查了利用裂项相消法求数列的和,关键是对数列通项的列项的掌握,是中档题.
分析:
(1)设等差数列{an}的公差为d,由a1,a4,a8成等比数列得到首项和公差的关系,再由数列{an}的前10项和为45列式求出首项和公差,则答案可求;(2)利用裂项相消法求出数列{bn}的前n项和为Tn,由可求出数列{an}的公差.
设等差数列{an}的公差为d,由a1,a4,a8成等比数列可得,.即,∴,而d≠0,∴a1=9d.(1)由数列{an}的前10项和为45,得,即90d+45d=45,故d=,a1=3,故数列{an}的通项公式为;(2),则数列{bn}的前n项和为Tn===.故数列{an}的公差d=1或d=-1.
点评:
本题考查了等差数列的通项公式,考查了利用裂项相消法求数列的和,关键是对数列通项的列项的掌握,是中档题.
看了 在公差不为0的等差数列{an...的网友还看了以下:
数列知识解答下面的题已知数列an的首项a1=a(a是常数,a不等于-1),an=2an-1(n-1为 2020-03-30 …
已知甲数是已、丙、丁三数之和的2分之1,已数是甲、丙、丁三数之和的3分之1,(接下去的在补充里)接 2020-06-03 …
地亩计算中已知长度及亩数怎样求宽度那位朋友知道这个公式,就是已知道了地的亩数,并知道这块地的长度, 2020-07-17 …
甲乙丙三个数的平均数是3.2,已知甲数是4.1,已数是1.8,丙数是其实已经有人回答了,但连个人是 2020-07-19 …
相差量除以单位一的量(一个数未知)单位一的量已知,求分率的量(或相反)比例与路程时间速度相结合.相 2020-07-20 …
有没有这样的数学书呢?我上完初中就退学了,已经有三年了。数学知识基本上都忘光了,最近想补一下数学知识 2020-11-14 …
甲已俩数相除,商是5无余数,已知甲数比已数大168,被除数是多少? 2020-11-20 …
一道小学试题求答:已知数A比数B多360,数A除已数B的商是5,问数A乘已数B的积是多少? 2020-11-20 …
1.甲.乙.丙三个数之和为239.已知已数比甲数的3倍多5,丙数比已数的2倍少6.这三个数分别是多少 2020-12-17 …
已知甲数除以乙数等于3.6,甲数减已数等于6.5,甲已两数各是多少?(不用方程来解) 2021-01-23 …