早教吧作业答案频道 -->数学-->
设各项均为正数的数列{an}的前n项和为Sn,满足,且a2,a5,a14构成等比数列.(1)证明:;(2)求数列{an}的通项公式;(3)证明:对一切正整数n,有.
题目详情
设各项均为正数的数列{a n }的前n项和为S n ,满足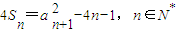 ,且a 2 ,a 5 ,a 14 构成等比数列.
,且a 2 ,a 5 ,a 14 构成等比数列.
(1)证明: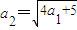 ;
;
(2)求数列{a n }的通项公式;
(3)证明:对一切正整数n,有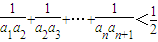 .
.
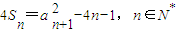 ,且a 2 ,a 5 ,a 14 构成等比数列.
,且a 2 ,a 5 ,a 14 构成等比数列.(1)证明:
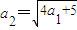 ;
;(2)求数列{a n }的通项公式;
(3)证明:对一切正整数n,有
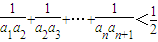 .
.▼优质解答
答案和解析
分析:
(1)对于,令n=1即可证明;(2)利用,且,(n≥2),两式相减即可求出通项公式.(3)由(2)可得=.利用“裂项求和”即可证明.
(1)当n=1时,,∵(2)当n≥2时,满足,且,∴,∴,∵an>0,∴an+1=an+2,∴当n≥2时,{an}是公差d=2的等差数列.∵a2,a5,a14构成等比数列,∴,,解得a2=3,由(1)可知,,∴a1=1∵a2-a1=3-1=2,∴{an}是首项a1=1,公差d=2的等差数列.∴数列{an}的通项公式an=2n-1.(3)由(2)可得式=.∴
点评:
熟练掌握等差数列与等比数列的通项公式、“裂项求和”、通项与前n项和的关系an=Sn-Sn-1(n≥2)是解题的关键.
分析:
(1)对于,令n=1即可证明;(2)利用,且,(n≥2),两式相减即可求出通项公式.(3)由(2)可得=.利用“裂项求和”即可证明.
(1)当n=1时,,∵(2)当n≥2时,满足,且,∴,∴,∵an>0,∴an+1=an+2,∴当n≥2时,{an}是公差d=2的等差数列.∵a2,a5,a14构成等比数列,∴,,解得a2=3,由(1)可知,,∴a1=1∵a2-a1=3-1=2,∴{an}是首项a1=1,公差d=2的等差数列.∴数列{an}的通项公式an=2n-1.(3)由(2)可得式=.∴
点评:
熟练掌握等差数列与等比数列的通项公式、“裂项求和”、通项与前n项和的关系an=Sn-Sn-1(n≥2)是解题的关键.
看了 设各项均为正数的数列{an}...的网友还看了以下:
一道线性代数证明题:A为n阶实矩阵,其特征值全为实数,且AA'=A'A 证明:A=A' (A'是A 2020-04-05 …
一道有序数对电影院里的座位按“x排y号”编排,小明的座位简记为(12,6),小菲的座位简记为(12 2020-06-03 …
下列关于票据的各项表述中,符合规定的有()。A.票据的中文大写金额数字应用正楷或行书填写B.票据的 2020-06-09 …
A.B.C三个站在同一直线上,B到A.C两站的距离相等,小明和小强分别从A.C两站同时出发,相向而 2020-06-10 …
若一个自然数A能被7,11或13整除,证明这个自然数的末三位所表示的数于末三位前的数若一个自然数A 2020-06-16 …
青岛市2014年市区环境空气质量优良天数达到262天,优良率达到了71.8%.与之前同期相比,重污 2020-07-19 …
请问,原子序数的符号“Z”与质量数符号“A”分别是什么的缩写?原子序数明明是“atomicnumb 2020-07-21 …
一列纵队若干人。从前往后数,明明是第8名,从后往前数是第7名。这列纵队共有多少人要列式 2020-07-22 …
勾股定理的问题3、4、5是一组勾股数,3k、4k、5k是一组勾股数吗?若a、b、c为一组勾股数,那 2020-07-26 …
4位正整数中间2数相同,首数比末数小3,将前2数交换,后2数交换,得的新数比原大7155,原4位数 2020-07-30 …