早教吧作业答案频道 -->数学-->
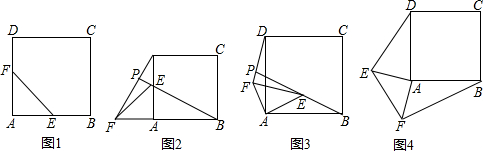
如图1,E,F分别是正方形ABCD的边AB,AD的中点.AB=4,且将△AEF绕点A逆时针旋转.(1)如图2,当△AEF绕点A逆时针旋转90°时,连结DF,BE,延长BE交DF于点P,求BP的长.(2)如图3,在△AEF绕点A
题目详情
如图1,E,F分别是正方形ABCD的边AB,AD的中点.AB=4,且将△AEF绕点A逆时针旋转.
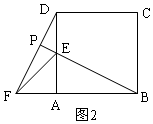
(1)如图2,当△AEF绕点A逆时针旋转90°时,连结DF,BE,延长BE交DF于点P,求BP的长.
(2)如图3,在△AEF绕点A逆时针旋转过程中,直线BE,DF相交于点P,则线段BE,DF有怎样的关系?利用图3的位置加以证明.
(3)如图4,当△AEF旋转到图4位置时,△AED与△AFB的面积关系如何?利用图4证明.
(1)如图2,当△AEF绕点A逆时针旋转90°时,连结DF,BE,延长BE交DF于点P,求BP的长.
(2)如图3,在△AEF绕点A逆时针旋转过程中,直线BE,DF相交于点P,则线段BE,DF有怎样的关系?利用图3的位置加以证明.
(3)如图4,当△AEF旋转到图4位置时,△AED与△AFB的面积关系如何?利用图4证明.

▼优质解答
答案和解析
 (1)∵四边形ABCD为正方形,
(1)∵四边形ABCD为正方形,
∴AB=AD=4,∠DAB=90°,
如图1,∵E,F分别是正方形ABCD的边AB,AD的中点,
∴AE=AF=2,
由旋转得:图2中的AE=AF=2,
在△AFD和△AEB中,
∵
,
∴△AFD≌△AEB(SAS),
∴∠ADF=∠ABE,
∵∠AEB=∠DEP,
∴∠DPE=∠DAB=90°,
在Rt△AEB中,AE=2,AB=4,
由勾股定理得:BE=
=2
,
cos∠ABE=
=
,
∴
=
,
BP=
;
(2)BE=DF且BE⊥DF,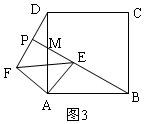
理由如下:
由旋转得:∠EAB=∠FAD,
∵AE=AF,AB=AD,
∴△AEB≌△AFD,
∴BE=DF,∠FDA=∠ABE,
∵∠PMD=∠AMB,
∴∠DPM=∠MAB=90°,
∴BP⊥DF,即BE⊥DF;
(3)如图4,△AED与△AFB的面积相等,理由是:
过F作FH⊥AB,交BA延长线于H,过E作EG⊥AD于G,
∵∠EAF=90°,
∴∠EAH+∠FAH=90°,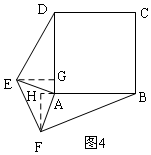
∵∠HAD=90°,
∴∠EAH+∠EAG=90°,
∴∠FAH=∠EAG,
∵AE=AF,∠EGA=∠AHF=90°,
∴△AEG≌△AFH,
∴EG=FH,
∵S△AED=
AD•EG,
S△ABF=
AB•FH,
∵AB=AD,
∴S△AED=S△AFB.
 (1)∵四边形ABCD为正方形,
(1)∵四边形ABCD为正方形,∴AB=AD=4,∠DAB=90°,
如图1,∵E,F分别是正方形ABCD的边AB,AD的中点,
∴AE=AF=2,
由旋转得:图2中的AE=AF=2,
在△AFD和△AEB中,
∵
|
∴△AFD≌△AEB(SAS),
∴∠ADF=∠ABE,
∵∠AEB=∠DEP,
∴∠DPE=∠DAB=90°,
在Rt△AEB中,AE=2,AB=4,
由勾股定理得:BE=
| 22+42 |
| 5 |
cos∠ABE=
| BP |
| BF |
| AB |
| BE |
∴
| BP |
| 2+4 |
| 4 | ||
2
|
BP=
12
| ||
| 5 |
(2)BE=DF且BE⊥DF,

理由如下:
由旋转得:∠EAB=∠FAD,
∵AE=AF,AB=AD,
∴△AEB≌△AFD,
∴BE=DF,∠FDA=∠ABE,
∵∠PMD=∠AMB,
∴∠DPM=∠MAB=90°,
∴BP⊥DF,即BE⊥DF;
(3)如图4,△AED与△AFB的面积相等,理由是:
过F作FH⊥AB,交BA延长线于H,过E作EG⊥AD于G,
∵∠EAF=90°,
∴∠EAH+∠FAH=90°,

∵∠HAD=90°,
∴∠EAH+∠EAG=90°,
∴∠FAH=∠EAG,
∵AE=AF,∠EGA=∠AHF=90°,
∴△AEG≌△AFH,
∴EG=FH,
∵S△AED=
| 1 |
| 2 |
S△ABF=
| 1 |
| 2 |
∵AB=AD,
∴S△AED=S△AFB.
看了如图1,E,F分别是正方形AB...的网友还看了以下:
怎样使用matlab解下面的代数方程?急.syms a b c d e;2*b^2=a^2+c^2 2020-05-16 …
在关系模式R(D,E,G)中,存在函数依赖关系{E→D,(D,G)→E},则候选码为________ 2020-05-23 …
在关系模式R(D,E,G)中,存在函数依赖关系{E→D,(D,G)→E},则候选码为【】。 2020-05-23 …
A.(-d|d)d*E(-d|d)d*|(-d|d)*.d*(ε|E(-d|d)d*)B.(-d|d 2020-05-26 …
A.(-d|d)d*E(-d|d)d*|(-d|d)d*.d*[ε|E(-d|d)d*]B.(-d| 2020-05-26 …
三角形ABC中,AD垂直于BC,垂足为点D(D在BC边上),BE垂直于AC,垂足为点E,M为AB边 2020-06-03 …
main(){unionEXAMPLE{struct{intx,y;}in;inta,b;}e;e 2020-06-12 …
在五环图案内,分别填写五个数a,b,c,d,e,如图(1),其中a,b,c是三个连续偶数(a<b< 2020-08-02 …
“我们可以得到A和B分别与C、D、E之间的关系”这句话用英语怎么表达“我们可以得到A和B分别与C、D 2020-12-25 …
已知A、B、C、D、E五种物质之间存在以下的转化关系.其中A、C两种物质的组成元素相同,且常温下为液 2021-01-22 …