如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=2;正确的是()A.4个B.3个C.2个D.1个
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=
;正确的是( )2 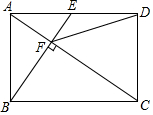
A. 4个
B. 3个
C. 2个
D. 1个
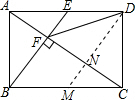 如图,过D作DM∥BE交AC于N,
如图,过D作DM∥BE交AC于N,∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴
| AE |
| BC |
| AF |
| CF |
∵AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AF |
| CF |
| 1 |
| 2 |
∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=
| 1 |
| 2 |
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故③正确;
设AE=a,AB=b,则AD=2a,
由△BAE∽△ADC,有
| b |
| a |
| 2a |
| b |
| 2 |
∴tan∠CAD=
| CD |
| AD |
| b |
| 2a |
| ||
| 2 |
故选B.
设a>0,f(x)=e^x/a+a/e^x是R上的偶函数,求a值.∵f(x)=e^x/a+a/e^ 2020-05-17 …
若a/b=c/d=e/f,则下列各式中正确的是().A.e/f=ac/bdB.e/f=(a+c+e 2020-06-06 …
(2005•盐城一模)如图所示为人体体温调节示意图.请根据下图回答有关问题:(1)图中T→E→N→ 2020-06-10 …
已知f(x)在x=a可导,且f(x)>0,n为自然数,求lim[f(a+1/n)/f(a)]^n( 2020-06-12 …
高数导数问题.设f(x)=(e^x-e^a)g(x)在x=a处可导,则函数g(x)应该满足条件是? 2020-07-20 …
△ABC的内切圆⊙O与AB、BC、CA分别相切于D、E、F,∠A=60°,OA=2√3,设BC长为 2020-08-01 …
△ABC的内切圆⊙O与AB、BC、CA分别相切于D、E、F,∠A=60°,OA=2√3,设BC长为 2020-08-01 …
三元一次方程组a*x+b*y+c*z+d=0,e*x+f*y+g*z+h=0,i*x+j*y+k* 2020-08-03 …
EXCEL循环或计算问题。F=A+B+C+D+E。(A.B.C.D.E.F.均要大于零)E=A*10 2020-11-01 …
为什么不是f(a)>f(0)/e^af(x)位定义在R上的可导函数,且f'(x)>f(x),对任为什 2020-11-03 …