早教吧作业答案频道 -->数学-->
在矩形ABCD中,AB=8,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF,(点E、F为折痕与矩形ABCD边的交点),再将纸片还原.(1)若点P落在矩形ABCD的边AB上(如图①).①当点P与点A重
题目详情
在矩形ABCD中,AB=8,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF,(点E、F为折痕与矩形ABCD边的交点),再将纸片还原.
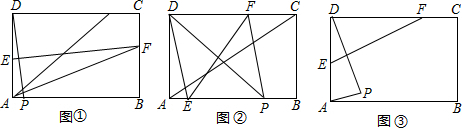
(1)若点P落在矩形ABCD的边AB上(如图①).
①当点P与点A重合时,∠DEF___;当点E与点A重合时,∠DEF=___;
②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=7时菱形DEPF的边长.
(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值.
(1)若点P落在矩形ABCD的边AB上(如图①).
①当点P与点A重合时,∠DEF___;当点E与点A重合时,∠DEF=___;
②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=7时菱形DEPF的边长.
(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值.

▼优质解答
答案和解析
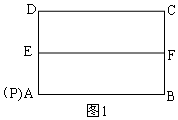 (1)①当点P与点A重合时,如图1,
(1)①当点P与点A重合时,如图1,
∴EF是AD的中垂线,
∴∠DEF=90°,
当点E与点A重合时,如图2,
此时∠DEF=
∠DAB=45°,
故答案为:90°,45°;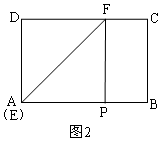
②当点E在AB上,点F在DC上时,如图3,
∵EF是PD的中垂线,
∴DO=PO,EF⊥PD,
∵四边形ABCD是矩形,
∴DC∥AB,
∴∠FDO=∠EPO,
∵∠DOF=∠EOP,
∴△DOF≌△POE(ASA),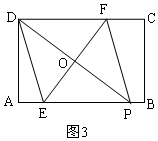
∴DF=PE,
∵DF∥PE,
∴四边形DEPF是平行四边形,
∵EF⊥PD,
∴▱DEPF为菱形,
当AP=7时,设菱形的边长为x,则AE=7-x,DE=x,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴62+(7-x)2=x2,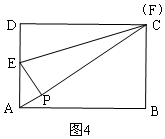
x=
,
∴当AP=7时,设菱形的边长为
;
(2)若点P落在矩形ABCD的内部,且点E、F分别在AD、DC边上,
如图4,当F与C重合,点P在对角线AC上时,AP有最小值,
由折叠得:CD=PC=8,
由勾股定理得:AC=
=10,
∴AP=10-8=2,
则AP的最小值是2.
 (1)①当点P与点A重合时,如图1,
(1)①当点P与点A重合时,如图1,∴EF是AD的中垂线,
∴∠DEF=90°,
当点E与点A重合时,如图2,
此时∠DEF=
| 1 |
| 2 |
故答案为:90°,45°;

②当点E在AB上,点F在DC上时,如图3,
∵EF是PD的中垂线,
∴DO=PO,EF⊥PD,
∵四边形ABCD是矩形,
∴DC∥AB,
∴∠FDO=∠EPO,
∵∠DOF=∠EOP,
∴△DOF≌△POE(ASA),

∴DF=PE,
∵DF∥PE,
∴四边形DEPF是平行四边形,
∵EF⊥PD,
∴▱DEPF为菱形,
当AP=7时,设菱形的边长为x,则AE=7-x,DE=x,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴62+(7-x)2=x2,

x=
| 85 |
| 14 |
∴当AP=7时,设菱形的边长为
| 85 |
| 14 |
(2)若点P落在矩形ABCD的内部,且点E、F分别在AD、DC边上,
如图4,当F与C重合,点P在对角线AC上时,AP有最小值,
由折叠得:CD=PC=8,
由勾股定理得:AC=
| 62+82 |
∴AP=10-8=2,
则AP的最小值是2.
看了在矩形ABCD中,AB=8,A...的网友还看了以下:
如图(7)连结多边形不相邻的两个顶点的线段叫做多边形的对角线.容易看出,三角形没有对角线四边形有两条 2020-03-30 …
1、四边形,五边形、六边形各有几条对角线?从中得出什么规律?2、根据规律求七边形的对角线的数量.3 2020-05-14 …
关于n边形(1)从n边形的一个顶点出发可做多少条对角线?,从n边形n个顶点出发可做多少条对角线?出 2020-05-14 …
在多边形中,连结不相邻的两个顶点的线段叫做多边形的对角线.(1)分别说出四边形、五边形、六边形、各 2020-05-14 …
1,平行四边形的对边(),并且().2,从平行四边形一条边上的一点到它对边的()是平行四边形的高1 2020-05-21 …
下列命题错误的是()A.平行四边形的对边相等B.两组对边分别相等的四边形是平行四边形C.对角线相等 2020-05-23 …
怎么用对角线相等来证明四边形是平行四边形拜托各位大神怎么样用四边形的对角线相等,来证明一个四边形是 2020-06-04 …
多边形及其内角和,要求用初一的方式来解题,快,1.三角形的对角线有条,四边形的对角线有条,五边形的 2020-06-05 …
已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半以四边形ABCD 2020-06-06 …
“因为四边形ABCD是矩形,所以四边形ABCD的对角线相等”以上推理的大前提是()A.矩形都是四边 2020-06-13 …