设函数f（x）=lnxx，关于x的方程[f（x）]2+mf（x）-1=0有三个不同的实数解，则实数m的取值范围是（）A.（-∞，e-1e）B.（e-1e，+∞）C.（0，e）D.（1，e）

Question

设函数f（x）=

(lnx)/(x)，关于x的方程[f（x）]²+mf（x）-1=0有三个不同的实数解，则实数m的取值范围是（　　）

A. （-∞，e-

(1)/(e)）

B. （e-

(1)/(e)，+∞）

C. （0，e）

D. （1，e）

Answer 1

f′（x）=(1-lnx)/(x2)，
∴当x>e时，f′（x）<0，当0<x<e时，f′（x）>0，
∴f（x）在（0，e]上单调递增，在（e，+∞）上单调递减．
∴f_max（x）=f（e）=(1)/(e)．
作出f（x）的大致函数图象如下：

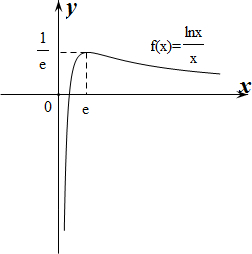
由图象可知当0<k<(1)/(e)时，f（x）=k有两解，
当k≤0或k=(1)/(e)时，f（x）=k有一解，当k>(1)/(e)时，f（x）=k无解．
令g（x）=x²+mx-1，则g（f（x））有三个零点，
∴g（x）在（0，(1)/(e)）上有一个零点，在（-∞，0]∪{(1)/(e)}上有一个零点．
∵g（x）的图象开口向上，且g（0）=0，∴g（x）在（-∞，0）上必有一个零点，
∴g（(1)/(e)）>0，即(1)/(e2)+(m)/(e)-1>0，
解得m>e-(1)/(e)．
故选B．