早教吧作业答案频道 -->数学-->
如图,某港口一天6时到18时的水深变化曲线近似满足函数y=sin(π6x+φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为.
题目详情
如图,某港口一天6时到18时的水深变化曲线近似满足函数y=sin(
x+φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为___.
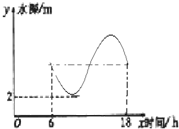
| π |
| 6 |

▼优质解答
答案和解析
由题意可得当sin(
x+φ)取最小值-1时,
函数取最小值ymin=-1+k=2,解得k=3,
∴y=sin(
x+φ)+3,
∴当sin(
x+φ)取最大值1时,
函数取最大值ymax=1+3=4,
故答案为:4.
| π |
| 6 |
函数取最小值ymin=-1+k=2,解得k=3,
∴y=sin(
| π |
| 6 |
∴当sin(
| π |
| 6 |
函数取最大值ymax=1+3=4,
故答案为:4.
看了如图,某港口一天6时到18时的...的网友还看了以下:
直线型需求曲线的斜率不变,因此其价格弹性也不变,该说法是否正确?求解析如题. 2020-04-05 …
《微观经济学》,直线型需求曲线的斜率不变,因此其价格弹性也不变.这种说法是否正确? 2020-04-05 …
f(z)在简单闭曲线C围成的闭区域D上解析,证明f(z)的绝对值不超过他在C上的最大值M复变函数f 2020-05-15 …
直线型需求曲线的斜率不变,因此其价格弹性也不变,该说法是否正确?弹性公式是e=(△Q/Q)/(△P 2020-05-15 …
将曲线log2x+log2y=2沿x、y轴-分别向右平移两个单位,向上平移一个单位,此时直线x+y 2020-06-06 …
将曲线log2x+log2y=2沿x、y轴-分别向右平移两个单位,向上平移一个单位,此时直线x+y 2020-06-06 …
设函数φ(y)具有连续导数,在围绕原点的任意分段光滑简单闭曲线L上,曲线积分∮Lφ(y)dx+2x 2020-06-27 …
梯度方向不是法线方向?在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜 2020-07-31 …
vb程序选择题在子过程Sub…EndSub中使用的形式参数可以是()。A.常数、简单变量、数组变量和 2020-11-20 …
如图是关于近代以来主要资本主义国家主流经济理论影响力演变曲线图,读图完成下列要求.指出曲线A、B分别 2020-11-28 …