早教吧作业答案频道 -->数学-->
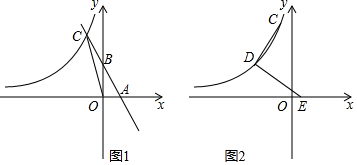
如图1,直线y=-2x+4交x轴、y轴于A、B两点,交双曲线y=kx(x<0)于C点,△AOC的面积为6.(1)求双曲线的解析式.(2)如图2,D为双曲线y=kx(x<0)上一点,连结CD,将线段CD绕点D顺时针旋转
题目详情
如图1,直线y=-2x+4交x轴、y轴于A、B两点,交双曲线y=
(x<0)于C点,△AOC的面积为6.
(1)求双曲线的解析式.
(2)如图2,D为双曲线y=
(x<0)上一点,连结CD,将线段CD绕点D顺时针旋转90°得线段DE,点E恰好落在x轴上,求点E的坐标.
| k |
| x |
(1)求双曲线的解析式.
(2)如图2,D为双曲线y=
| k |
| x |

▼优质解答
答案和解析
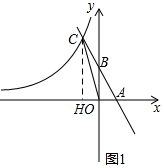 (1)过C作CH⊥x轴于H,
(1)过C作CH⊥x轴于H,
直线y=-2x+4中,令y=0,则x=2,
∴A(2,0),即AO=2,
∵△AOC的面积为6,
∴
×AO×CH=6,
∴
×2×CH=6,
∴CH=6,即点C的纵坐标为6,
直线y=-2x+4中,当y=6时,6=-2x+4,
解得x=-1,
∴C(-1,6),
代入y=
(x<0)可得,k=-1×6=-6,
∴双曲线的解析式为y=-
;
(2)过点D作DF⊥x轴于F,过C作CG⊥DF于G,则∠G=∠DFE=90°,
由旋转可得,CD=DE,∠CDE=90°,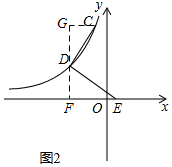
∴∠CDG=∠DEF,
在△DCG和△EDF中,
,
∴△DCG≌△EDF(AAS),
∴CG=DF,DG=EF,
设D(a,-
),则DF=-
,FO=-a,
∵C(-1,6),
∴CG=-1-a,
∴DF=-1-a,
∴-
=-1-a,
解得a=-3或a=2(舍去),
∴DF=-1+3=2,DG=GF-DF=6-2=4,
∴EF=4,
又∵FO=3,
∴OE=4-3=1,
∴E(1,0).
 (1)过C作CH⊥x轴于H,
(1)过C作CH⊥x轴于H,直线y=-2x+4中,令y=0,则x=2,
∴A(2,0),即AO=2,
∵△AOC的面积为6,
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴CH=6,即点C的纵坐标为6,
直线y=-2x+4中,当y=6时,6=-2x+4,
解得x=-1,
∴C(-1,6),
代入y=
| k |
| x |
∴双曲线的解析式为y=-
| 6 |
| x |
(2)过点D作DF⊥x轴于F,过C作CG⊥DF于G,则∠G=∠DFE=90°,
由旋转可得,CD=DE,∠CDE=90°,

∴∠CDG=∠DEF,
在△DCG和△EDF中,
|
∴△DCG≌△EDF(AAS),
∴CG=DF,DG=EF,
设D(a,-
| 6 |
| a |
| 6 |
| a |
∵C(-1,6),
∴CG=-1-a,
∴DF=-1-a,
∴-
| 6 |
| a |
解得a=-3或a=2(舍去),
∴DF=-1+3=2,DG=GF-DF=6-2=4,
∴EF=4,
又∵FO=3,
∴OE=4-3=1,
∴E(1,0).
看了如图1,直线y=-2x+4交x...的网友还看了以下:
将3x2y+|x2+y|表示成计算机程序表达式为()A.SQR(3*x^2*y)+ABS(x/(2 2020-06-09 …
下列各项中注音有误的一项是()A.伺候cì殷红yīnhóng岩层yáncéngB.赝品yànpǐn 2020-06-28 …
反比例函数与二次函数在同一平面直角坐标系中的大致图象如图所示,则它们的解析式可能分别是()A.y= 2020-07-12 …
利用芳香烃X和链烃Y可以合成紫外线吸收剂BAD,BAD的结构简式为(如图1):已知G不能发生银镜反 2020-07-19 …
下列各式中,不能用平方差公式计算的是()A.(x-y)(-x+y)B.(-x-y)(-x+y)C. 2020-07-31 …
下列各式中,不能用平方差公式计算的是[]A.(x﹣y)(﹣x+y)B.(﹣x﹣y)(﹣x+y)C. 2020-07-31 …
下列各式中,不能用平方差公式计算的是[]A.(x﹣y)(﹣x+y)B.(﹣x﹣y)(﹣x+y)C. 2020-07-31 …
分式1x+y,2xx2−y2,y2(y−x)的最简公分母是()A.(x2-y2)(x-y)B.(x 2020-08-01 …
下列式子正确的是()A.x-(y-z)=x-y-zB.-(x-y+z)=-x-y-zC.x+2y-2 2020-10-30 …
选出下列字音有误的一项:()A.湮没yān筵席yán赝品yànB.窈窈yǎotiǎo揶揄yéyú陶冶 2020-11-07 …