已知如图，直线l1：y1=-34x+m与y轴交于A（0，6），直线l2：y2=kx+1分别与x轴交于点B（-2，0），与y轴交于点C．两条直线相交于点D，连接AB．求：（1）直线l1、l2的解析式；（2）求△ABD的面积；

Question

已知如图，直线l1：y1=-(3)/(4)x+m与y轴交于A（0，6），直线l₂：y₂=kx+1分别与x轴交于点B（-2，0），与y轴交于点C．两条直线相交于点D，连接AB．求：

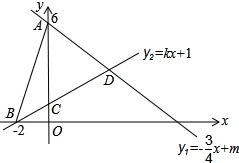
（1）直线l₁、l₂的解析式；
（2）求△ABD的面积；
（3）在x轴上是否存在一点P，使得S△ABP=(4)/(3)S△ABD？若存在，求出点P的坐标；若不存在，说明理由．

Answer 1

（1）∵直线l1：y1=-(3)/(4)x+m与y轴交于A（0，6），
∴m=6，
∴y₁=-(3)/(4)x+6，
∵y₂=kx+1分别与x轴交于点B（-2，0），
∴-2k+1=0，
∴k=(1)/(2)，
∴y₂=(1)/(2)x+1；
（2）令y₂=(1)/(2)x+1中x=0，求出y=1，
∴点C坐标为（0，1），
联立

y=-(3)/(4)x+6

y=(1)/(2)x+1

，
解得x=4，y=3，
∴点D的坐标为（4，3），
∴S_△ACB=(1)/(2)AC•BO=(1)/(2)×（6-1）×2=5，
S_△ACD=(1)/(2)×5×4=10，
∴S_△ABD=S_△ACB+S_△ACB=5+10=15；
（3）设点P坐标为（m，0），
当点P在B点的右侧时，
BP=m+2，
S_△ABP=(1)/(2)BP•AO=(1)/(2)×（m+2）×6=(4)/(3)×15，
解得m=(14)/(3)，
则点P坐标为（(14)/(3)，0），
当点P在B点的左侧时，
BP=-2-m，
S_△ABP=(1)/(2)BP•AO=(1)/(2)×（-2-m）×6=(4)/(3)×15，
解得m=-(26)/(3)，
则点P坐标为（-(26)/(3)，0），
综上点P的坐标为（(14)/(3)，0）或（-(26)/(3)，0）．