早教吧作业答案频道 -->数学-->
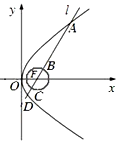
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x-1)2+y2=14于点A,B,C,D四点,则9|AB|+4|CD|的最小值为.
题目详情
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x-1)2+y2=
于点A,B,C,D四点,则9|AB|+4|CD|的最小值为___.
| 1 |
| 4 |

▼优质解答
答案和解析
∵y2=4x,焦点F(1,0),准线 l0:x=-1
由定义得:|AF|=xA+1,
又∵|AF|=|AB|+
,∴|AB|=xA+
同理:|CD|=xD+
,
当l⊥x轴时,则xD=xA=1,∴9|AB|+4|CD|=
.
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,xA+xD=1,
∴9|AB|+4|CD|=
+9xA+4xD≥
+2
=
.
综上所述4|AB|+9|CD|的最小值为
.
故答案为:
.
由定义得:|AF|=xA+1,
又∵|AF|=|AB|+
| 1 |
| 2 |
| 1 |
| 2 |
同理:|CD|=xD+
| 1 |
| 2 |
当l⊥x轴时,则xD=xA=1,∴9|AB|+4|CD|=
| 39 |
| 2 |
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,xA+xD=1,
∴9|AB|+4|CD|=
| 13 |
| 2 |
| 13 |
| 2 |
| 4×9xAxD |
| 37 |
| 2 |
综上所述4|AB|+9|CD|的最小值为
| 37 |
| 2 |
故答案为:
| 37 |
| 2 |
看了如图,已知抛物线y2=4x的焦...的网友还看了以下:
因式分解3题(1)(1-1/2^2)(1-1/3^2)(1-1/4^2).(1-1/10^2)(2 2020-05-17 …
问几道关于分式方程的数学题已知1/(x-1)=2,则2/(x-1)+x-1的值是多少?若方程1/( 2020-06-06 …
已知1/x²+1/y²=a,xy=b,则(x+y)²为多少?∵1/x²+1/y²=a,xy=b∴1 2020-06-29 …
初一数学问题28.1/a-1+1/a+1-2/a^2-129.3-x/2-x÷(x+2-5/x-2 2020-07-22 …
已知x+y=-4,xy=-12.,求y+1/x+1+x+1/y+1的值.已知1/x-1/y=5,求 2020-07-28 …
先阅读下列材料,再解答下列问题.已知1+x+x2+x3+x4+x5=0,求x6的值.解:∵1+x+x 2020-10-31 …
已知1/x-1/x+1=1/x(x+1)求1/x(x+1)+1/(x+1)(x+2).1/(x+99 2020-10-31 …
1.若x/3=y/4=z/5,则分式(x+y)/(x-2y+3z)的值.2.若x=y/2=z/5,且 2020-10-31 …
1,已知1/x+1/y=1/6,1/y+1/z=1/9,1/z+1/x=1/15,求xy+yz+zx 2020-11-07 …
1.已知1/x+1/y=1/x+y,求y/x+x/y2.已知非零实数abc满足a^+b^+c^=1, 2020-12-07 …