早教吧作业答案频道 -->数学-->
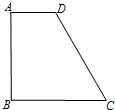
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,∠BCD=60°,CD=5.将梯形ABCD绕点A旋转后得到梯形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,当点B1落在边CD上时,点D1恰好落在CD的延长线上,
题目详情
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,∠BCD=60°,CD=5.将梯形ABCD绕点A旋转后得到梯形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,当点B1落在边CD上时,点D1恰好落在CD的延长线上,那么DD1的长为___.

▼优质解答
答案和解析
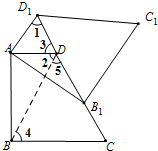 如图,将梯形ABCD绕点A旋转后得到梯形AB1C1D1,连接BD,
如图,将梯形ABCD绕点A旋转后得到梯形AB1C1D1,连接BD,
由旋转得:AD=AD1,AB=AB1,∠DAD1=∠BAB1,
∴∠DAB=∠D1AB1,且∠1=∠3,
在△DAB和△D1AB1中,
,
∴△DAB≌△D1AB1(SAS),
∴∠1=∠2,
∴∠2=∠3,
∵AD∥BC,
∴∠2=∠4,
设∠1=∠2=∠3=∠4=α,则∠5=180°-∠4-∠C=120°-α,
∵∠2+∠3+∠5=180°,
∴α+α+120°-α=180°,
解得α=60°,
∴∠1=∠2=∠3=∠4=60°,
∴△ADD1、△BCD都是等边三角形,
∴BD=CD=5,∠ABD=30°,
∴Rt△ABD中,AD=
BD=
,
∴DD1=AD=
.
故答案为:
 如图,将梯形ABCD绕点A旋转后得到梯形AB1C1D1,连接BD,
如图,将梯形ABCD绕点A旋转后得到梯形AB1C1D1,连接BD,由旋转得:AD=AD1,AB=AB1,∠DAD1=∠BAB1,
∴∠DAB=∠D1AB1,且∠1=∠3,
在△DAB和△D1AB1中,
|
∴△DAB≌△D1AB1(SAS),
∴∠1=∠2,
∴∠2=∠3,
∵AD∥BC,
∴∠2=∠4,
设∠1=∠2=∠3=∠4=α,则∠5=180°-∠4-∠C=120°-α,
∵∠2+∠3+∠5=180°,
∴α+α+120°-α=180°,
解得α=60°,
∴∠1=∠2=∠3=∠4=60°,
∴△ADD1、△BCD都是等边三角形,
∴BD=CD=5,∠ABD=30°,
∴Rt△ABD中,AD=
| 1 |
| 2 |
| 5 |
| 2 |
∴DD1=AD=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
看了如图,在直角梯形ABCD中,A...的网友还看了以下:
读图完成问题1.位于东西半球分界线上的点是2.同时位于东半球、北半球、中纬度的点有A.F点B.D点 2020-04-23 …
1.在平行四边形ABCD中,将E,F点分别从A,C点以相同速度向B,D点移动,将G,H点分别从A, 2020-05-20 …
已知角mon,以o为圆心,以不同的半径画两条弧分别交om,on于a,c,b,d点,连接ad,bc交 2020-05-23 …
科研人员对某海洋食用生物进行研究,得出了与种群密度相关的出生率和死亡率的变化,如图所示,请据图判断 2020-06-11 …
科研人员对某草原一种哺乳动物的种群进行研究,得出了与种群密度相关的出生率和死亡率的变化,如图所示。 2020-06-11 …
如图表示根、茎对生长素浓度变化的反应曲线,有关叙述不正确的是()A.根、茎两种器官对生长素的反应敏 2020-06-26 …
如图所示,在y轴上关于O点对称的A、B两点有等量同种点电荷+Q,在x轴上C点有点电荷-Q,且CO= 2020-06-29 …
常温下,向1LpH=10的KOH溶液中持续通入CO2,与溶液中水电离出的c(OH-)与通入的CO2 2020-07-29 …
BA垂直BD,CD垂直MN,垂足分别是B.D点,角FDC等于角EBA.判断CD与AB的位置关系 2020-07-30 …
图中各点方位描述正确的是()A.A点在B点的东南方向B.D点在A点的正南方向C.C点在A点的东南方 2020-07-31 …