早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,椭圆C的标准方程为(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B,设原点到直线BF的距离为d1,F到l的距离为d2,若d2=,则椭圆C的离心率为
题目详情
在平面直角坐标系xOy中,椭圆C的标准方程为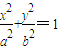 (a>b>0),右焦点为F,右准线为l,短轴的一个端点为B,设原点到直线BF的距离为d 1 ,F到l的距离为d 2 ,若d 2 =
(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B,设原点到直线BF的距离为d 1 ,F到l的距离为d 2 ,若d 2 = ,则椭圆C的离心率为 .
,则椭圆C的离心率为 .
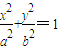 (a>b>0),右焦点为F,右准线为l,短轴的一个端点为B,设原点到直线BF的距离为d 1 ,F到l的距离为d 2 ,若d 2 =
(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B,设原点到直线BF的距离为d 1 ,F到l的距离为d 2 ,若d 2 = ,则椭圆C的离心率为 .
,则椭圆C的离心率为 .▼优质解答
答案和解析
分析:
根据“d2=”结合椭圆的半焦距,短半轴,长半轴构成直角三角形,再由等面积法可得d1=,从而得到a与b的关系,可求得,从而求出离心率.
如图,准线l:x=,d2=,由面积法得:d1=,若d2=,则,整理得a2-ab-=0,两边同除以a2,得+()-=0,解得.∴e==.故答案为:.
点评:
本题主要考查椭圆的几何性质,即通过半焦距,短半轴,长半轴构成的直角三角形来考查其离心率,还涉及了等面积法.
分析:
根据“d2=”结合椭圆的半焦距,短半轴,长半轴构成直角三角形,再由等面积法可得d1=,从而得到a与b的关系,可求得,从而求出离心率.
如图,准线l:x=,d2=,由面积法得:d1=,若d2=,则,整理得a2-ab-=0,两边同除以a2,得+()-=0,解得.∴e==.故答案为:.
点评:
本题主要考查椭圆的几何性质,即通过半焦距,短半轴,长半轴构成的直角三角形来考查其离心率,还涉及了等面积法.
看了在平面直角坐标系xOy中,椭圆...的网友还看了以下:
如图,在正方体ABCD-A1B1C1D1中,求证:(1)对角线B1D⊥平面A1C1B;老师证明了H 2020-05-16 …
小明为研究动能大小与哪些因素有关设计了如图实验,让小球静止从斜面上滚下后与固定在右端的弹簧碰撞,斜 2020-06-08 …
枝条的形态学上端为平面,下端要削成斜面这个到底是怎么样嘛? 2020-06-23 …
机械方面的判断对错只要机件有对称平面,其投影图均可画成半剖视图对吗?局部剖视图上的波浪线不因画在轮 2020-07-05 …
设O为△ABC的外心,平面上一点P使OP=OA+OB+OC,则P为△ABC的()A外心B内心C重心 2020-07-30 …
在空间几何中,如何判断三棱锥的“重心”,“内心”,“外心”,“垂心”?平面几何中(也就是三角形中) 2020-07-30 …
读《某商业中心平面图》(图7-6-5),完成下列问题。(1)图中所示商业中心的组织形式是,该商业中 2020-08-01 …
如图甲所示,一平行板电容器极板长l=10cm,宽a=8cm,两极板间距为d=4cm,距极板右端12处 2020-11-03 …
如图为株洲市湘江两岸中心平面图,回答4~5题:此图缺失了比例尺,只知道从中心广场到长江广场实际距离为 2020-11-12 …
英语翻译中心线的平面位移标高皮带轮轮宽中心平面偏移传动轴水平度纵向横向连轴器两轴芯径向位移两轴线倾斜 2020-11-26 …