如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
①四边形A2B2C2D2是矩形;②四边形A4B4C4D4是菱形;③四边形A5B5C5D5的周长是
,④四边形AnBnCnDn的面积是a+b 4
.ab 2n+1 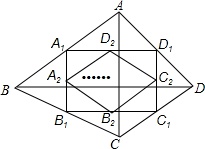
A. 1个
B. 2个
C. 3个
D. 4个
 ∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,
∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
∵AC丄BD,∴四边形A1B1C1D1是矩形,
∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
故本选项错误;
②由①知,四边形A2B2C2D2是菱形;
∴根据中位线定理知,四边形A4B4C4D4是菱形;
故本选项正确;
③根据中位线的性质易知,A5B5=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形A5B5C5D5的周长是2×
| 1 |
| 8 |
| a+b |
| 4 |
故本选项正确;
④∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnCnDn的面积是
| ab |
| 2n+1 |
故本选项正确.
综上所述,②③④正确.
故选C.
设A,B是n阶方阵,下列式子正确的是()(A)AB=BA(B)A^2-B^2=(A+B)(A-B)( 2020-03-30 …
设A,B,A+B均为n阶可逆矩阵,则(A-1+B-1)-1=() A.A-1+BB.A+B C.B 2020-04-05 …
若不等式组x+a≥0 1-2x>x-2 有解,则a的取值范围是?A.a>-1 B.a≥-1 C.a 2020-05-15 …
一道应该挺简单的数学题.函数f(x)=3ax-2a+1在〔-1,1〕上存在一个零点,则a的取值范围 2020-05-16 …
集合A={x∈R∣y=lgx},B={x∈Rl2x2^-2(1-a)x+a(1-a)>0},D=A 2020-06-06 …
求证:1\a(a+d)+1\(a+d)(a+2d)+.+1\[a+(n-2)d][a+(n-1)d 2020-06-12 …
若函数y=f(x)的定义域是[0,1],则函数f(x+a)+f(2x+a)(0<a<1)的定义域是 2020-07-25 …
小刚和小玲同时从A点出发,沿一个长方形的场地相背而行,小刚按A→B→C→D→A顺序走,小玲按A→D→ 2020-11-21 …
某企业去年7月份产值为a万元,8月份比7月份减少了10%,9月份比8月份增加了15%,则9月份的产值 2020-12-31 …
如果正数数列{an}为等差数列,公差d>0那么下列数列中为等差数列的是A.{根号a(n)}B.{根号 2021-02-04 …