设函数f（x）=|ex-e2a|，若f（x）在区间（-1，3-a）内的图象上存在两点，在这两点处的切线相互垂直，则实数a的取值范围是．

Question

设函数f（x）=|e^x-e^2a|，若f（x）在区间（-1，3-a）内的图象上存在两点，在这两点处的切线相互垂直，则实数a的取值范围是___．

Answer 1

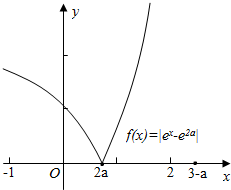当x≥2a时，f（x）=|e^x-e^2a|=e^x-e^2a，此时为增函数，
当x<2a时，f（x）=|e^x-e^2a|=-e^x+e^2a，此时为减函数，
即当x=2a时，函数取得最小值0，设两个切点为M（x₁，f（x₁）），N（（x₂，f（x₂）），
由图象知，当两个切线垂直时，必有，x₁<2a2，
即-1<2a<3-a，得-(1)/(2)<a<1，
∵k₁k₂=f′（x₁）f′（x₂）=ex1•(-ex2)=-ex1+x2=-1，
则ex1+x2=1，即x₁+x₂=0，
∵-1<x₁<0，∴0<x₂<1，且x₂>2a，
∴2a<1，解得a<(1)/(2)，
综上-(1)/(2)<a<(1)/(2)，
故答案为：（-(1)/(2)，(1)/(2)）