早教吧作业答案频道 -->数学-->
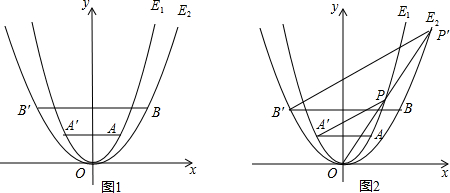
已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y轴的对称点分别为点A′,B′.(1)求m的值及抛物线E2所表示的二次函数的表达式;(2)如图1,
题目详情
已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
(1)求m的值及抛物线E2所表示的二次函数的表达式;
(2)如图1,在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)如图2,P为第一象限内的抛物线E1上与点A不重合的一点,连接OP并延长与抛物线E2相交于点P′,求△PAA′与△P′BB′的面积之比.
(1)求m的值及抛物线E2所表示的二次函数的表达式;
(2)如图1,在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)如图2,P为第一象限内的抛物线E1上与点A不重合的一点,连接OP并延长与抛物线E2相交于点P′,求△PAA′与△P′BB′的面积之比.

▼优质解答
答案和解析
(1)∵抛物线E1经过点A(1,m),
∴m=12=1.
∵抛物线E2的顶点在原点,可设它对应的函数表达式为y=ax2(a≠0),
又∵点B(2,2)在抛物线E2上,
∴2=a×22,
解得:a=
,
∴抛物线E2所对应的二次函数表达式为y=
x2.
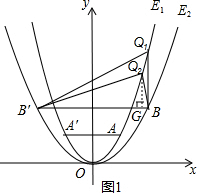 (2)如图1,假设在第一象限内,抛物线E1上存在点Q,使得△QBB′为直角三角形,
(2)如图1,假设在第一象限内,抛物线E1上存在点Q,使得△QBB′为直角三角形,
由图象可知直角顶点只能为点B或点Q.
①当点B为直角顶点时,过B作QB⊥BB′交抛物线E1于Q,
则点Q与B的横坐标相等且为2,将x=2代入y=x2得y=4,
∴点Q的坐标为(2,4).
②当点Q为直角顶点时,则有QB′2+QB2=B′B2,过点Q作GQ⊥BB′于G,
设点Q的坐标为(t,t2)(t>0),
则有(t+2)2+(t2-2)2+(2-t)2+(t2-2)2=16,
整理得:t4-3t2=0,
∵t>0,∴t2-3=0,解得t1=
,t2=-
(舍去),
∴点Q的坐标为(
,3),
综合①②,存在符合条件的点Q坐标为(2,4)与(
,3);
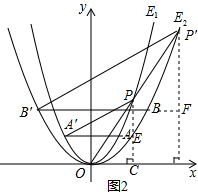 (3)如图2,过点P作PC⊥x轴,垂足为点C,PC交直线AA′于点E,
(3)如图2,过点P作PC⊥x轴,垂足为点C,PC交直线AA′于点E,
过点P′作P′D⊥x轴,垂足为点D,P′D交直线BB′于点F,
依题意可设P(c,c2)、P′(d,
d2) (c>0,c≠q),
∵tan∠POC=tan∠P′OD,
∴
=
,
∴d=2c.
∵AA′=2,BB′=4,
∴
=
=
=
∴m=12=1.
∵抛物线E2的顶点在原点,可设它对应的函数表达式为y=ax2(a≠0),
又∵点B(2,2)在抛物线E2上,
∴2=a×22,
解得:a=
| 1 |
| 2 |
∴抛物线E2所对应的二次函数表达式为y=
| 1 |
| 2 |
 (2)如图1,假设在第一象限内,抛物线E1上存在点Q,使得△QBB′为直角三角形,
(2)如图1,假设在第一象限内,抛物线E1上存在点Q,使得△QBB′为直角三角形,由图象可知直角顶点只能为点B或点Q.
①当点B为直角顶点时,过B作QB⊥BB′交抛物线E1于Q,
则点Q与B的横坐标相等且为2,将x=2代入y=x2得y=4,
∴点Q的坐标为(2,4).
②当点Q为直角顶点时,则有QB′2+QB2=B′B2,过点Q作GQ⊥BB′于G,
设点Q的坐标为(t,t2)(t>0),
则有(t+2)2+(t2-2)2+(2-t)2+(t2-2)2=16,
整理得:t4-3t2=0,
∵t>0,∴t2-3=0,解得t1=
| 3 |
| 3 |
∴点Q的坐标为(
| 3 |
综合①②,存在符合条件的点Q坐标为(2,4)与(
| 3 |
 (3)如图2,过点P作PC⊥x轴,垂足为点C,PC交直线AA′于点E,
(3)如图2,过点P作PC⊥x轴,垂足为点C,PC交直线AA′于点E,过点P′作P′D⊥x轴,垂足为点D,P′D交直线BB′于点F,
依题意可设P(c,c2)、P′(d,
| 1 |
| 2 |
∵tan∠POC=tan∠P′OD,
∴
| c2 |
| c |
| ||
| d |
∴d=2c.
∵AA′=2,BB′=4,
∴
| S△PAA′ |
| SP′BB′ |
| ||
|
| ||||
|
看了已知抛物线E1:y=x2经过点...的网友还看了以下:
如图,已知直线a‖b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为如图,已 2020-05-16 …
在反比例函数y=x分之8(x>0)的图像上有两点A,B,且点A的纵坐标为2,点B的横坐标为2在反比 2020-06-14 …
已知椭圆x^2/a^2+y^2/b^2=1(a>b>0)的长轴长和短轴长之差是2√2-2,且右焦点 2020-06-21 …
探讨数轴上两点之间的距离已知数轴上有两个点A、B,求A、B之间的距离:(1)当A为+2,B为+3时 2020-06-27 …
数轴上点A为-2,点B位10,若点C也是数轴上一点,点C到点A的距离是点C到点B的距离的三分之一, 2020-07-30 …
若实数a,b,c在数轴上所对应点分别为A,B,C,a为2的算术平方根,b=3,C点是A点关于B点的 2020-07-30 …
1.直线的斜率为2,在X轴上的截距为-3,则直线的方程为他与直线X+Y-3=0的交点座标为2.点A 2020-07-30 …
在反比例函数y=8/x(X大于零)的图象上有两点a,b,且点a的纵坐标为2,点b的横坐标为2,分别 2020-08-01 …
初一数学题关于平面直角坐标在方格纸上有A,B两点,若以点B为原点建立平面直角坐标系,则点A的坐标为 2020-08-01 …
在反比例函数y=8/x(x>0)的图像上有两点A、B,且点A的纵坐标为2,点B的横坐标为2,分别过 2020-08-01 …
 扫描下载二维码
扫描下载二维码
