早教吧作业答案频道 -->数学-->
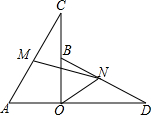
如图,OA=OB,OC=OD,∠AOB=∠COD=90°,M,N分别为AC,BD的中点,连接MN,ON,求证:∠MNO=45°.
题目详情
如图,OA=OB,OC=OD,∠AOB=∠COD=90°,M,N分别为AC,BD的中点,连接MN,ON,求证:∠MNO=45°.

▼优质解答
答案和解析
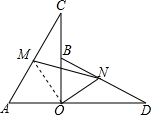 证明:连接OM,
证明:连接OM,
在△AOC与△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD,∠C=∠D,
∵M,N分别为AC,BD的中点,
∴OM=
AC,ON=
BD,
∴OM=ON,
∴OM=CM=ON=DN,
∴∠MOC=∠C=∠D=∠MOD,
∴∠COM+∠BON=90°,
∴△MPN是等腰直角三角形,
∴∠MNO=45°.
 证明:连接OM,
证明:连接OM,在△AOC与△BOD中,
|
∴△AOC≌△BOD,
∴AC=BD,∠C=∠D,
∵M,N分别为AC,BD的中点,
∴OM=
| 1 |
| 2 |
| 1 |
| 2 |
∴OM=ON,
∴OM=CM=ON=DN,
∴∠MOC=∠C=∠D=∠MOD,
∴∠COM+∠BON=90°,
∴△MPN是等腰直角三角形,
∴∠MNO=45°.
看了如图,OA=OB,OC=OD,...的网友还看了以下:
在9.6、9.4、9.4、9.7、9.4、9.8、9.7、9.2这组数中,中位数是()A.9.4B 2020-04-07 …
六年级分数混合运算35道不要1.3/7×49/9-4/32.8/9×15/36+1/273.12× 2020-04-08 …
初二数学题我们来证明“2=3”.这是西班牙流行的一个“诡辩”,人们用下述方法“证明”这一结论.因为 2020-05-16 …
1.化简3(sina+cosa)^4+6(sina-cosa)^2+4(sin^6a+cos^6a 2020-05-16 …
帮我破解下这串数字什么意思9(2)4(3)6(2)2(1)4(3)3(1)4(3)9(1)6(3) 2020-05-17 …
2003年4月6日,天大建筑公司参与了海瑞公司关于其办公楼建设工程招投标活动,天大公司通过现场竞标 2020-07-11 …
口算24÷4=7+63=9×4=36÷6=56÷8=28+6=7×5=36+4=63÷9=64÷8 2020-07-17 …
请告诉我这个证明过程中哪里错了证明2=3因为4-10=9-15所以4-10+25/4=9-15+2 2020-07-17 …
一.观察下列式子:2×4+1=9=3^26×8+1=49=7^214×16+1=225=15^2… 2020-07-19 …
已知动直线l:(m+3)x-(m+2)y+m=0,圆C:(x-3)^2+(y-4)^2=9求证:无论 2021-01-12 …