如图，在矩形ABCD中，AB=4，AD=2，点M是AB上一动点，点N是对角线AC上一动点，则MN+BN的最小值为．

Question

如图，在矩形ABCD中，AB=4，AD=2，点M是AB上一动点，点N是对角线AC上一动点，则MN+BN的最小值为___．

Answer 1

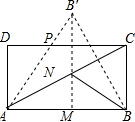如图，作点B关于AC的对称点B′，过点B′作B′M⊥AB于M，交AC于N，
连接AB′交DC于P，连接BN，
∵四边形ABCD是矩形，
∴DC∥AB，
∴∠BAC=∠PCA，
∵点B关于AC的对称点是B′，
∴∠PAC=∠BAC，
∴∠PAC=∠PCA，
∴PA=PC．
令PA=x，则PC=x，PD=8-x．
在Rt△ADP中，∵PA²=PD²+AD²，
∴x²=（4-x）²+2²，
∴x=(5)/(2)，
∵cos∠B′AM=cos∠APD，
∴AM：AB′=DP：AP，
∴AM：4=1.5：2.5，
∴AM=(12)/(5)，
∴B′M=√(AB′2-AM2)=(16)/(5)，
∴MN+BN的最小值=(16)/(5)．
故答案为：(16)/(5)．