早教吧作业答案频道 -->数学-->
如图是二次函数y=ax2+bx=c的图象,则a、b、c满足()A、a>0,b>0,c>0B、a>0,b<0,c>0C、a>0,b>0,c<0D、a>0,b<0,c<0
题目详情
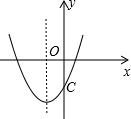 如图是二次函数y=ax 2 +bx=c的图象,则a、b、c满足( )
如图是二次函数y=ax 2 +bx=c的图象,则a、b、c满足( )| A、a>0,b>0,c>0 |
| B、a>0,b<0,c>0 |
| C、a>0,b>0,c<0 |
| D、a>0,b<0,c<0 |
▼优质解答
答案和解析
考点:
二次函数图象与系数的关系
专题:
计算题
分析:
根据抛物线开口方向确定a的符号;根据抛物线的对称轴的位置得到a、b同号,则b>0;根据抛物线与y轴的交点位置确定c的符号.
∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴的左侧,∴a、b同号,∴b>0,∵抛物线与y轴交点在x轴下方,∴c<0.故选C.
点评:
本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);△决定抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
考点:
二次函数图象与系数的关系
专题:
计算题
分析:
根据抛物线开口方向确定a的符号;根据抛物线的对称轴的位置得到a、b同号,则b>0;根据抛物线与y轴的交点位置确定c的符号.
∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴的左侧,∴a、b同号,∴b>0,∵抛物线与y轴交点在x轴下方,∴c<0.故选C.
点评:
本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);△决定抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
看了如图是二次函数y=ax2+bx...的网友还看了以下:
已知a、b是有理数,ab的绝对值等于—ab(ab不等于0),a+b的绝对值等于a的绝对值+b,用数 2020-05-15 …
1.m-2的相反数是6,那么m的值是( ).A.4 B.-4 C.8 D.-82.已知|m+3|+ 2020-05-16 …
进行下列数的数制转换(213)D=()B=()H=()O(69.625)D=()B=()H=()O 2020-05-21 …
初三比例式计算.如题.已知a/b=c/d(bd不等于0).判断下列比例式是否成立.并说明理由.a- 2020-06-10 …
若a>b>0,c<d<0,则一定有()若a>b>0,c<d<0,则一定有()A.a/d>b/cB. 2020-06-12 …
如果abcd>0,a>c,bcd<0,则有()A.a>0,b<0,c>0,d>0B.a<0,b<0 2020-07-09 …
已知二次函数的图像,求结论,已知二次函数y=ax²+bx+c(a≠0)的图像,下列四个结论①b<0 2020-07-19 …
下列说法错误的是()A.命题“若x2-4x+3=0,则x=3”的逆否命题是:“若x≠3,则x2-4 2020-08-01 …
已知a>0,b>0,c>0,b²-4ac>0,则抛物线y=ax²+bx+c经过的象限()此题答案是一 2020-11-01 …
(2013•永昌县)如图是在平行线间的五个图形,它们的面积相比较()A.a>b>c>d>eB.a<b 2020-12-22 …