如图，某日的钱塘江观潮信息如表：按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离s（千米）与时间t（分钟）的函数关系用图3表示，其中：“11：40时甲地‘交叉潮’的潮头离

Question

如图，某日的钱塘江观潮信息如表：

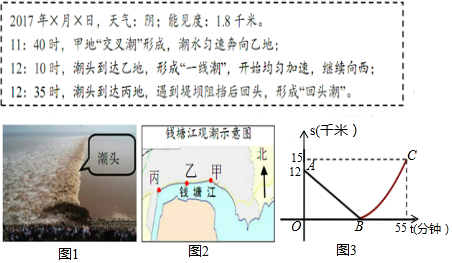
按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离s（千米）与时间t（分钟）的函数关系用图3表示，其中：“11：40时甲地‘交叉潮’的潮头离乙地12千米”记为点A（0，12），点B坐标为（m，0），曲线BC可用二次函数s=(1)/(125)t²+bt+c（b，c是常数）刻画．
（1）求m的值，并求出潮头从甲地到乙地的速度；
（2）11：59时，小红骑单车从乙地出发，沿江边公路以0.48千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？
（3）相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为0.48千米/分，小红逐渐落后，问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度v=v₀+(2)/(125)（t-30），v₀是加速前的速度）．

Answer 1

（1）由题意可知：m=30；
∴B（30，0），
潮头从甲地到乙地的速度为：(12)/(30)=0.4千米/分钟；

（2）∵潮头的速度为0.4千米/分钟，
∴到11：59时，潮头已前进19×0.4=7.6千米，
设小红出发x分钟与潮头相遇，
∴0.4x+0.48x=12-7.6，
∴x=5
∴小红5分钟与潮头相遇，

（3）把（30，0），C（55，15）代入s=(1)/(125)t²+bt+c，
解得：b=-(2)/(25)，c=-(24)/(5)，
∴s=(1)/(125)t²-(2)/(25)t-(24)/(5)
∵v₀=0.4，
∴v=(2)/(125)（t-30）+(2)/(5)，
当潮头的速度达到单车最高速度0.48千米/分钟，
此时v=0.48，
∴0.48=(2)/(125)（t-30）+(2)/(5)，
∴t=35，
当t=35时，
s=(1)/(125)t²-(2)/(25)t-(24)/(5)=(11)/(5)，
∴从t=35分（12：15时）开始，潮头快于小红速度奔向丙地，小红逐渐落后，当小红仍以0.48千米/分的速度匀速追赶潮头．
设她离乙地的距离为s₁，则s₁与时间t的函数关系式为s₁=0.48t+h（t≥35），
当t=35时，s₁=s=(11)/(5)，代入可得：h=-(73)/(5)，
∴s₁=(12)/(25)t-(73)/(5)
最后潮头与小红相距1.8千米时，即s-s₁=1.8，
∴(1)/(125)t²-(2)/(25)t-(24)/(5)-(12)/(25)t+(73)/(5)=1.8
解得：t=50或t=20（不符合题意，舍去），
∴t=50，
小红与潮头相遇后，按潮头速度与潮头并行到达乙地用时6分钟，
∴共需要时间为6+50-30=26分钟，
∴小红与潮头相遇到潮头离她1.8千米外共需要26分钟，