早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠B=Rt∠,直角边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边A→B→C→A的方向运动,运动时间为t(秒).(1)求AB与BC的
题目详情
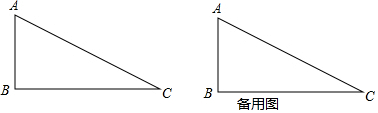
如图,在Rt△ABC中,∠B=Rt∠,直角边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为
时运动时间t的值;
(3)点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为
| 10 |
(3)点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.

▼优质解答
答案和解析
(1)∵x2-7x+12=(x-3)(x-4)=0,
∴x1=3或x2=4.
则AB=3,BC=4,
(2)由题意得32+(t-3)2=
,
∴t1=4,t2=2(舍去)
则t=4时,AP=
,
(3)存在点P,使△ABP是等腰三角形.
在Rt△ABC中,AB=3,BC=4,根据勾股定理得,AC=5,
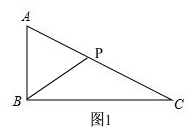
①当AP=AB=3时,如图1,
 ,
,
∴PC=AC-AP=5-3=2,
∴点P运动路程是AB+BC+PC=3+4+2=9,
∴t=9(秒).
②当BP=BA=3时,如图2,
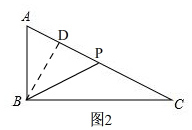
当P在AC上时,
过点B作BD⊥AC于D,
根据△ABC的面积得,
BD•AC=
AB•BC,
∴BD=
在Rt△ABD中,AB=3,BD=
,
根据勾股定理得,AD=
,
∴PC=AC-2AD=
,
∴点P运动的路程为AB+BC+PC=3+4+
=
,
∴t=
(秒)
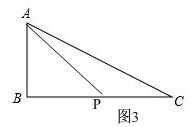
当P在BC上时,如图3,
 ,
,
∴点P运动的路程为AB+BP=3+3=6,
∴t=6(秒)
③当BP=AP (即P为AC中点时),
∴t=9.5(秒)
可知当t为9秒或9.5秒或6(秒)或
(秒)时,△ABP是等腰三角形.
∴x1=3或x2=4.
则AB=3,BC=4,
(2)由题意得32+(t-3)2=
| 10 |
∴t1=4,t2=2(舍去)
则t=4时,AP=
| 10 |
(3)存在点P,使△ABP是等腰三角形.
在Rt△ABC中,AB=3,BC=4,根据勾股定理得,AC=5,
①当AP=AB=3时,如图1,
 ,
,∴PC=AC-AP=5-3=2,
∴点P运动路程是AB+BC+PC=3+4+2=9,
∴t=9(秒).
②当BP=BA=3时,如图2,

当P在AC上时,
过点B作BD⊥AC于D,
根据△ABC的面积得,
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=
| 12 |
| 5 |
在Rt△ABD中,AB=3,BD=
| 12 |
| 5 |
根据勾股定理得,AD=
| 9 |
| 5 |
∴PC=AC-2AD=
| 7 |
| 5 |
∴点P运动的路程为AB+BC+PC=3+4+
| 7 |
| 5 |
| 42 |
| 5 |
∴t=
| 42 |
| 5 |
当P在BC上时,如图3,
 ,
,∴点P运动的路程为AB+BP=3+3=6,
∴t=6(秒)
③当BP=AP (即P为AC中点时),
∴t=9.5(秒)
可知当t为9秒或9.5秒或6(秒)或
| 42 |
| 5 |
看了如图,在Rt△ABC中,∠B=...的网友还看了以下:
有效役龄是指( )所经历的实际时间 A.从开始使用到技术落后被淘汰 B.从开始使用到予以报 2020-05-19 …
设备的经济寿命是指( )所经历的时间 A.从开始使用到经济上不合算 B.从开始使用到技术落 2020-05-19 …
从某批产品中,有放回的抽取产品两次,每次随机抽取1件,假设时间A:"...从某批产品中,有放回的抽 2020-06-13 …
在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.(1)实验操 2020-06-14 …
如图①,正方形abcd的边长为4㎝,点a'从点d出发以每秒1㎝的速度沿射线dc 2020-06-22 …
AB间的距离为s,质点从A点由静止出发沿直线运动到B点停止,在这段时间内,质点可以做匀速运动,也可 2020-07-10 …
如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B 2020-07-11 …
如图,P、Q两点表示的数分别是-20和20,动点A从点P向右运动,动点B从点Q出发,以每秒2个单位 2020-07-22 …
甲、乙两人同时A从点出发沿直线向B点走去.乙先到达B点,然后返回,在C点遇到甲后再次返回到达B点后 2020-07-24 …
(2012•白下区一模)如图,在平面直角坐标系中,x轴上一点A从点(-3,0)出发沿x轴向右平移, 2020-07-30 …