早教吧作业答案频道 -->物理-->
如图所示,一小球从平台上水平抛出,恰好落在临近平台的一倾角为α=53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8m,斜面顶端高H=20.8m,g=10m/s2,sin53°=0.
题目详情
如图所示,一小球从平台上水平抛出,恰好落在临近平台的一倾角为α=53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8m,斜面顶端高H=20.8m,g=10m/s2,sin 53°=0.8,cos 53°=0.6.则:
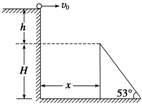
(1)小球水平抛出的初速度v0是多大?
(2)斜面顶端与平台边缘的水平距离x是多少?
(3)则小球离开平台后经多长时间t到达斜面底端?

(1)小球水平抛出的初速度v0是多大?
(2)斜面顶端与平台边缘的水平距离x是多少?
(3)则小球离开平台后经多长时间t到达斜面底端?
▼优质解答
答案和解析
(1)由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以
vy=v0tan53°
vy2=2gh
代入数据,得vy=4m/s,v0=3m/s
故小球的水平速度为3m/s;
(2)由vy=gt得t=0.4s
x=v0t=3×0.4=1.2m
(3)对物体受力分析,根据牛顿第二定律可得,
小球沿斜面做匀加速直线运动的加速度 a=gsin 53°,
初速度为平抛运动的末速度 v=
=
=5 m/s.
则
=vt′+
at′2
解得 t′=2s.(负值舍去)
所以t总=t+t′=2.4 s.
答:(1)小球水平抛出的初速度v0是3m/s;
(2)斜面顶端与平台边缘的水平距离x是1.2m;
(3)则小球离开平台后经2.4s时间t到达斜面底端.
vy=v0tan53°
vy2=2gh
代入数据,得vy=4m/s,v0=3m/s
故小球的水平速度为3m/s;
(2)由vy=gt得t=0.4s
x=v0t=3×0.4=1.2m
(3)对物体受力分析,根据牛顿第二定律可得,
小球沿斜面做匀加速直线运动的加速度 a=gsin 53°,
初速度为平抛运动的末速度 v=
| v0 |
| cos53° |
| 3 |
| 0.6 |
则
| H |
| sin53° |
| 1 |
| 2 |
解得 t′=2s.(负值舍去)
所以t总=t+t′=2.4 s.
答:(1)小球水平抛出的初速度v0是3m/s;
(2)斜面顶端与平台边缘的水平距离x是1.2m;
(3)则小球离开平台后经2.4s时间t到达斜面底端.
看了如图所示,一小球从平台上水平抛...的网友还看了以下:
下列单位换算过程中,正确的是()A.5.8m=5.8×100=580cmB.5.8dm=5.8×1 2020-04-07 …
下列单位换算过程中,正确的是()。A.5.8m=5.8×100=580cmB.5.8dm=5.8× 2020-04-07 …
下列用正数和负数表示意义相反的量,其中正确的是()A.如果+3.5m表示比海平面高3.5m,那么- 2020-05-14 …
下列用正数和负数表示意义相反的量,其中正确的是()A.如果+3.5m表示比海平面高3.5m,那么- 2020-05-14 …
有一位滑翔爱好者正在空中匀速向下滑翔已知水平方向上的风速为5.8m/s,如图在A点的他观察到C处塔 2020-05-17 …
楼梯设计题.某三层住宅楼,层高为2.9m,楼梯间开间2.7m,进深5.8m.墙厚240mm,室内外 2020-06-27 …
以知屋脊高度剪力墙高度中间平面间距怎么计算屋脊和剪力墙之间的长度?帮忙解决下谢谢已知屋脊高度5.8 2020-07-04 …
3.5mx5.8m的房间可以改成两个卧室吗?113个平方的房子,两室两厅,主卧加主厕3.5*5.8 2020-07-27 …
地震发生后,需要向灾区运送大量救灾物资,在物资转运过程中大量使用了如图所示的传送带.已知某传送带与水 2020-12-10 …
如图所示,一段铁路路基的横断面是等腰梯形,路基顶部BC的宽为9.8m,路基的高为5.8m,斜坡的坡度 2020-12-27 …