早教吧作业答案频道 -->物理-->
如图所示,用一根长为L=1.0m不可伸长的细绳,一端固定在天花板上的O点,另一端系一小球A,在O点的正下方钉一钉子B,质量为m=lKg的小球由水平位置静止释放,取g=l0m/s2.(1)在O点的正下
题目详情
如图所示,用一根长为L=1.0m不可伸长的细绳,一端固定在天花板上的O点,另一端系一小球A,在O点的正下方钉一钉子B,质量为m=lKg的小球由水平位置静止释放,取g=l0m/s2.
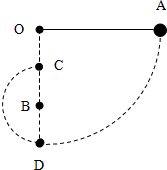
(1)在O点的正下方如果没有钉子B,小球摆到最低点D时,小球速度多大?(6分)细绳的拉力是多大?
(2)如果细绳的最大承受力为135N,要使细绳碰到B后小球能以B为圆心做完整的圆周运动,求钉子B离O点的可能距离.

(1)在O点的正下方如果没有钉子B,小球摆到最低点D时,小球速度多大?(6分)细绳的拉力是多大?
(2)如果细绳的最大承受力为135N,要使细绳碰到B后小球能以B为圆心做完整的圆周运动,求钉子B离O点的可能距离.
▼优质解答
答案和解析
(1)从A至D,应用动能定理,得:
mgL=
m
-0
变形得:vD=
=
=2
m/s
由圆周运动的规律及牛顿第二定律,有:
T-mg=m
代入数据,运算得:T=30N
(2)①当T为135N时,点B离O最远,设为S1,在最低点,由牛顿第二定律有:
T-mg=m
代入数值计算得:S1=0.84m
②设点B离O是最近的距离为S2,此时小球刚好能过最高点C.
在C点有,由牛顿第二定律有:mg=m
从D到C,应用动能定理有:
-mg•2(L-S2)=
m
-
m
由以上两式得:S2=0.6m
因此,B离O点的距离可能为0.6m至0.84m.
答:(1)小球摆到最低点D时,小球速度是2
m/s,细绳的拉力是30N.
(2)B离O点的距离可能为0.6m至0.84m.
mgL=
| 1 |
| 2 |
| v | 2 D |
变形得:vD=
| 2gL |
| 2×10×1 |
| 5 |
由圆周运动的规律及牛顿第二定律,有:
T-mg=m
| ||
| L |
代入数据,运算得:T=30N
(2)①当T为135N时,点B离O最远,设为S1,在最低点,由牛顿第二定律有:
T-mg=m
| ||
| L-S1 |
代入数值计算得:S1=0.84m
②设点B离O是最近的距离为S2,此时小球刚好能过最高点C.
在C点有,由牛顿第二定律有:mg=m
| ||
| L-S2 |
从D到C,应用动能定理有:
-mg•2(L-S2)=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 D |
由以上两式得:S2=0.6m
因此,B离O点的距离可能为0.6m至0.84m.
答:(1)小球摆到最低点D时,小球速度是2
| 5 |
(2)B离O点的距离可能为0.6m至0.84m.
看了如图所示,用一根长为L=1.0...的网友还看了以下: