早教吧作业答案频道 -->数学-->
四边形ABCD是菱形,点E在BC上,点F在AB上,点H在CD上,连接AE,FH交于点P,∠APF=∠ABC.(1)如图1,若∠ABC=90°,点F和点B重合,求证:AE=BH;(2)如图2.求证:AE=FH;(3)如图3,若AF+CH=BE,
题目详情
四边形ABCD是菱形,点E在BC上,点F在AB上,点H在CD上,连接AE,FH交于点P,∠APF=∠ABC.
(1)如图1,若∠ABC=90°,点F和点B重合,求证:AE=BH;
(2)如图2.求证:AE=FH;
(3)如图3,若AF+CH=BE,求∠B的度数.
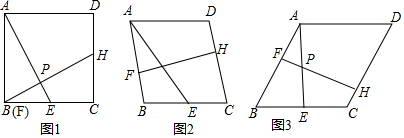
(1)如图1,若∠ABC=90°,点F和点B重合,求证:AE=BH;
(2)如图2.求证:AE=FH;
(3)如图3,若AF+CH=BE,求∠B的度数.

▼优质解答
答案和解析
(1)证明:如图1中,
∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∵∠APF=∠ABC=90°,
∴∠BAE+∠ABP=90°,∠ABP+∠CBH=90
∴∠BAE=∠CBH,
在△ABE和△BCH中,
,
∴△ABE≌△BCH,
∴AE=BH.
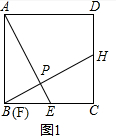
(2)证明:如图2中,延长CB到N,使得AN=AE,作HM∥BC交AB于M.
则四边形ADHM是平行四边形,AD=HM,
∵四边形ABCD是菱形,
∴AB=AD=HM,
∵HM∥CN,
∴∠HMF=∠ABN,
∵∠APF=∠ABC,∠PAF=∠BAE,
∴∠AFP=∠AEB=∠N,
∴△ABN≌△HMF,
∴AN=HF,
∵AE=AN,
∴AE=HF.
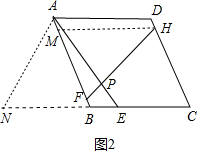
(3) 如图3中,在CB取一点N,使得AN=AE,作FM∥BC交CD于M.
则四边形ADMF是平行四边形,AD=FM,AF=DM,
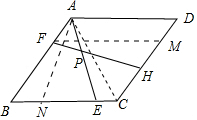
由(1)可知△ABN≌△FMH,
BN=HM,
∵BC=CD,AF+CH=DM+CH=BE,
∴CE=HM=BN,
在△ANB和△AEC中,
,
∴△ANB≌△AEC,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠B=60°.

∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∵∠APF=∠ABC=90°,
∴∠BAE+∠ABP=90°,∠ABP+∠CBH=90
∴∠BAE=∠CBH,
在△ABE和△BCH中,
|
∴△ABE≌△BCH,
∴AE=BH.
(2)证明:如图2中,延长CB到N,使得AN=AE,作HM∥BC交AB于M.
则四边形ADHM是平行四边形,AD=HM,

∵四边形ABCD是菱形,
∴AB=AD=HM,
∵HM∥CN,
∴∠HMF=∠ABN,
∵∠APF=∠ABC,∠PAF=∠BAE,
∴∠AFP=∠AEB=∠N,
∴△ABN≌△HMF,
∴AN=HF,
∵AE=AN,
∴AE=HF.
(3) 如图3中,在CB取一点N,使得AN=AE,作FM∥BC交CD于M.
则四边形ADMF是平行四边形,AD=FM,AF=DM,

由(1)可知△ABN≌△FMH,
BN=HM,
∵BC=CD,AF+CH=DM+CH=BE,
∴CE=HM=BN,
在△ANB和△AEC中,
|
∴△ANB≌△AEC,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠B=60°.
看了四边形ABCD是菱形,点E在B...的网友还看了以下:
多元复合函数求导,SOS~朋友们,在这部分我有点晕菜了,请您帮我理下思路吧?在求导时很重要的,求你 2020-05-21 …
如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM 2020-06-23 …
如图,△ABE与△ACD都是等边三角形,△AEC旋转后能与△ABD重合,EC与BD相交于点F,求如 2020-06-27 …
把一张矩形纸片ABCD按如图所示折叠,使A点与点E重合,点C与点F重合(E,F两点均在BD上)折痕 2020-07-10 …
把一张矩形纸片ABCD按如图所示折叠,使A点与点E重合,点C与点F重合(E,F两点均在BD上)折痕 2020-07-10 …
闰年的一年中,月份构成的集合为A,每月天数构成集合为B,f为月份与这个天数的对应法则,求集合B,并 2020-07-15 …
已知集合A={x|x平方+(a-1)x+b=0}={a},幂函数f(x)经过(a,b),(1)求集 2020-08-01 …
闰年的一年中,月份构成的集合为A,每月天数构成的集合为B,f为月份与这个月天数的对应法则,求集合B 2020-08-02 …
斜面上物体合力求法斜面上物体合力的求法公式是F-f=ma吗?为什么有些提的答案还要减去下滑力.请着重 2020-12-02 …
复合函数求导问题复合函数求导时,遇到一种函数通过不同形式两两组合可得到不同的结果时,应该如何解决例如 2020-12-13 …