早教吧作业答案频道 -->数学-->
如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.(1)求抛物线的解析式;(2)求△MCB的面积;(3)在抛物线上是否存在点P,使△PAB的
题目详情
如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.
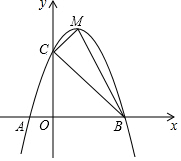
(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.

(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(1)∵A(-1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
∴
,
解方程组,得
,
故抛物线的解析式为y=-x2+4x+5;
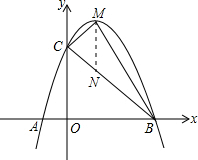 (2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=
(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=
MN•OB.
∵y=-x2+4x+5=-(x-5)(x+1)=-(x-2)2+9,
∴M(2,9),B(5,0),
由B、C两点的坐标易求得直线BC的解析式为:y=-x+5,
当x=2时,y=-2+5=3,则N(2,3),
则MN=9-3=6,
则S△MCB=
×6×5=15;
(3)在抛物线上存在点P,使△PAB的面积等于△MCB的面积.理由如下:
∵A(-1,0),B(5,0),
∴AB=6,
∵△PAB的面积=△MCB的面积,
∴
×6×|yP|=15,
∴|yP|=5,yP=±5.
当yP=5时,-x2+4x+5=5,解得x1=0,x2=4;
当yP=-5时,-x2+4x+5=-5,解得x3=2+
,x4=2-
.
故在抛物线上存在点P1(0,5),P2(4,5),P3(2+
,-5),P3(2-
,-5),使△PAB的面积等于△MCB的面积.
∴
|
解方程组,得
|
故抛物线的解析式为y=-x2+4x+5;
 (2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=
(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=| 1 |
| 2 |
∵y=-x2+4x+5=-(x-5)(x+1)=-(x-2)2+9,
∴M(2,9),B(5,0),
由B、C两点的坐标易求得直线BC的解析式为:y=-x+5,
当x=2时,y=-2+5=3,则N(2,3),
则MN=9-3=6,
则S△MCB=
| 1 |
| 2 |
(3)在抛物线上存在点P,使△PAB的面积等于△MCB的面积.理由如下:
∵A(-1,0),B(5,0),
∴AB=6,
∵△PAB的面积=△MCB的面积,
∴
| 1 |
| 2 |
∴|yP|=5,yP=±5.
当yP=5时,-x2+4x+5=5,解得x1=0,x2=4;
当yP=-5时,-x2+4x+5=-5,解得x3=2+
| 14 |
| 14 |
故在抛物线上存在点P1(0,5),P2(4,5),P3(2+
| 14 |
| 14 |
看了如图,抛物线y=ax2+bx+...的网友还看了以下:
从芮陈萵提取出来的对羟基苯乙酮()可用于制造利胆药.下列有关对羟基苯乙酮的说法错误的是()A.分于 2020-05-13 …
如a如b式成语如:如醉如痴 2020-05-17 …
问下关于高数左右极限的就是先比如大于a等于一个式子小于a等于一个式子等于a是个数然后把小于和大于a 2020-06-06 …
A如BC式词语,快A如BC式词语, 2020-06-08 …
若a大于b大于0,那么a的n次方大于b的n次方.为什么不等式两边含绝对值能平方去绝对值不等式这一章 2020-07-30 …
用大于号或小于号填空..求求大家啊(一元一次不等式)1.如果a大于b,那么a-b0(填大于或小于) 2020-08-01 …
对于二次八项式x如+如ax+a如可以直接用公式法分解为(x+a)如手形式,但对于二次八项式x如+如 2020-08-01 …
根号四是二次根式吗只是形如根号a这种形式的(a大于等于0)的二次根式吗?那根号下a²(a大于等于0 2020-08-02 …
不等式和区间的概念基础练习实数小于2,但不小于-1,用不等式可表示为.判断题若a>b,则a-1>b 2020-08-03 …
如果a大于b,则下列不等式成立的是A,ab大于0B,a-b大于0C,绝对值a大于绝对值b如果a大于 2020-08-03 …