早教吧作业答案频道 -->数学-->
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.(1)求证:△ABD∽△DCE;(2)设BD=x,AE=y,求y关于x的函数关系式.
题目详情
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.
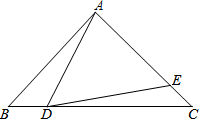
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式.

(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式.
▼优质解答
答案和解析
证明:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°
又∵∠ADB=∠DAC+∠C=∠DAC+45°,∠DEC=∠DAC+∠ADE=∠DAC+45°,
∴∠ADB=∠DEC,∴△ABD∽△DCE;
(2)(7分)∵∠BAC=90°,AB=AC=1
∴BC=
=
,
∴DC=BC-BD=
-x,
∵△ABD∽△DCE,
∴
=
,即
=
,
∴CE=
x-x2,
∴AE=AC-CE=1-(
x-x2)=x2-
x+1,
即y=x2-
x+1(其中0<x<
).
∴∠B=∠C=45°
又∵∠ADB=∠DAC+∠C=∠DAC+45°,∠DEC=∠DAC+∠ADE=∠DAC+45°,
∴∠ADB=∠DEC,∴△ABD∽△DCE;
(2)(7分)∵∠BAC=90°,AB=AC=1
∴BC=
| 12+12 |
| 2 |
∴DC=BC-BD=
| 2 |
∵△ABD∽△DCE,
∴
| CE |
| BD |
| DC |
| AB |
| CE |
| x |
| ||
| 1 |
∴CE=
| 2 |
∴AE=AC-CE=1-(
| 2 |
| 2 |
即y=x2-
| 2 |
| 2 |
看了已知:如图,△ABC中,∠BA...的网友还看了以下:
下列关于“机构波能传播…”的说法中,错误的是()A.波能传播介质质点B.波能传播机械振动的运动形式 2020-05-14 …
在下列各项中,不属于滚动预算方法的滚动方式的是( )。 A.逐年滚动方式B.逐季滚动方式C.逐月滚 2020-05-17 …
若要求生产时间最短,应采取的工序间移动方式为( )。A.顺序移动方式 B.平行移动方式C.平行顺序 2020-05-21 …
Windows NT操作系统提供了一个良好的用户交互界面,它是( )。A.菜单驱动方式B.图符驱动方 2020-05-24 …
以下不属于常见的软件架构模式的是(19)。A.产品库模式B.事件驱动模式C.C/S模式D.管理/过滤 2020-05-26 …
工序间搬运次数最少的零件移动方式是( )。A.顺序移动方式B.平行移动方式C.平行顺序移动 2020-05-30 …
单件小批企业多采用( )的时间组织方式。A.顺序移动方式 B.平行移动方式 C.平行顺序移 2020-05-30 …
下面不属于直接型质量流量计的是()流量计。A.差压式B.动量式C.速度式D.量热式 2020-05-31 …
社会工作者与志愿者的明显区别主要表现为()。A.提供社会服务B.活动方式C.专业技术能力D.处理问题 2020-06-04 …
选择电动机功率的主要依据是( )。 A.启动电流 B.启动方式 C.负载转矩的大小 D.环境条件 2020-06-07 …