早教吧作业答案频道 -->数学-->
如图,把一块含45°直角三角板的锐角顶点与正方形ABCD的顶点A重合.正方形ABCD固定不动,让三角板绕点A旋转.(1)当三角板绕点A旋转到如图①的位置时,含45°角的两边分别与正方形
题目详情
如图,把一块含45°直角三角板的锐角顶点与正方形ABCD的顶点A重合.正方形ABCD固定不动,让三角板绕点A旋转.
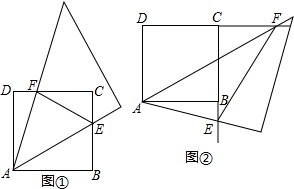
(1)当三角板绕点A旋转到如图①的位置时,含45°角的两边分别与正方形的边BC、DC交于点E、F,求证:EF=BE+DF;
(2)当三角板绕点A旋转到如图②的位置时,含45°角的两边分别与正方形的CB、DC两边的延长线交于点E、F.试写出EF、BE和DF三条线段满足的数量关系,不必证明.
(3)在图①中,当正方形ABCD的边长为6,EF=5,BE的长为___.

(1)当三角板绕点A旋转到如图①的位置时,含45°角的两边分别与正方形的边BC、DC交于点E、F,求证:EF=BE+DF;
(2)当三角板绕点A旋转到如图②的位置时,含45°角的两边分别与正方形的CB、DC两边的延长线交于点E、F.试写出EF、BE和DF三条线段满足的数量关系,不必证明.
(3)在图①中,当正方形ABCD的边长为6,EF=5,BE的长为___.
▼优质解答
答案和解析
(1)EF=BE+DF.
延长FD至G,使DG=BE,连接AG,如图①,
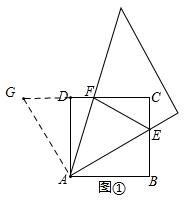
∵ABCD是正方形,
∴AB=AD,∠ABE=ADG=∠DAB=90°,
∴△ABE≌△ADG,
∴AE=AG,∠DAG=∠EAB,
∵∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠DAF+∠DAG=45°,
∴∠GAF=∠EAF=45°,
∵AF=AF,
∴△GAF≌△EAF,
∴EF=GF,
∴GF=DF+DG=DF+BE,
即:EF=DF+BE.
(2)EF=DF-BE.
在DC上截取DH=BE,连接AH,如图②,
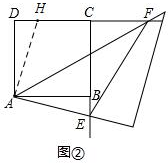
∵AD=AB,∠ADH=∠ABE=90°,
∴△ADH≌△ABE(SAS),
∴AH=AE,∠DAH=∠EAB,
∵∠EAF=∠EAB+∠BAF=45°,
∴∠DAH+∠BAF=45°,
∴∠HAF=45°=∠EAF,
∵AF=AF,
∴△HAF≌EAF(SAS),
∴HF=EF,
∵DF=DH+HF,
∴EF=DF-BE.
(3)如图③,
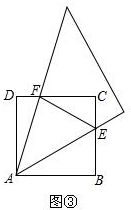
由(1)中结论可知:EF=DF+BE,
∵AB=BC=CD=AD=6,
设BE=x,则CE=6-x,
∵EF=5,
∴DF=5-x,
∴FC=1+x,
在Rt△CEF中,EF2=FC2+CE2,
∴25=(1+x)2+(6-x)2,
解得:x=2或x=3,
即BE的长为2或3.
延长FD至G,使DG=BE,连接AG,如图①,

∵ABCD是正方形,
∴AB=AD,∠ABE=ADG=∠DAB=90°,
∴△ABE≌△ADG,
∴AE=AG,∠DAG=∠EAB,
∵∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠DAF+∠DAG=45°,
∴∠GAF=∠EAF=45°,
∵AF=AF,
∴△GAF≌△EAF,
∴EF=GF,
∴GF=DF+DG=DF+BE,
即:EF=DF+BE.
(2)EF=DF-BE.
在DC上截取DH=BE,连接AH,如图②,

∵AD=AB,∠ADH=∠ABE=90°,
∴△ADH≌△ABE(SAS),
∴AH=AE,∠DAH=∠EAB,
∵∠EAF=∠EAB+∠BAF=45°,
∴∠DAH+∠BAF=45°,
∴∠HAF=45°=∠EAF,
∵AF=AF,
∴△HAF≌EAF(SAS),
∴HF=EF,
∵DF=DH+HF,
∴EF=DF-BE.
(3)如图③,

由(1)中结论可知:EF=DF+BE,
∵AB=BC=CD=AD=6,
设BE=x,则CE=6-x,
∵EF=5,
∴DF=5-x,
∴FC=1+x,
在Rt△CEF中,EF2=FC2+CE2,
∴25=(1+x)2+(6-x)2,
解得:x=2或x=3,
即BE的长为2或3.
看了如图,把一块含45°直角三角板...的网友还看了以下:
如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.(1)填空:∠ 2020-04-06 …
读六大板块示意图,完成17~20题板块发生碰撞运动时,会形成山脉、岛弧、深海沟,B处的山脉是有以下 2020-05-16 …
板块发生碰撞运动时,会形成山脉、岛弧、深海沟,B处的山脉是有以下两个板块碰撞形成的()A、亚欧板块 2020-05-16 …
25、根据板块学说,我国位于()板块?A、非洲板块B、印度洋板块C、亚欧板块D、太平洋板块26、在 2020-07-05 …
如图,在等腰梯形ABCD中,AD平行BC,BC=4AD=4根号2,∠B=45度,直角三角板含45度 2020-08-02 …
世界上最雄伟高大的喜马拉雅山脉形成的主要原因是()A.亚欧板块与太平洋板块碰撞抬升形成的B.亚欧板块 2020-12-06 …
科迪勒拉-安第斯山系的形成原因是()A.非洲板块、欧亚板块与印度洋板块碰撞形成的B.南极板块、太平洋 2020-12-25 …
科迪勒拉-安第斯山系的形成原因是()A.非洲板块、欧亚板块与印度洋板块碰撞形成的B.南极板块、太平洋 2020-12-25 …
科迪勒拉-安第斯山系的形成原因是[]A.非洲板块、欧亚板块与印度洋板块碰撞形成的B.南极板块、太平洋 2020-12-25 …
科迪勒拉-安第斯山系的形成原因是()A.非洲板块、欧亚板块与印度洋板块碰撞形成的B.南极板块、太平洋 2020-12-25 …