早教吧作业答案频道 -->数学-->
如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.(1)利用尺规作图补全图形;(要求:保留作图痕迹,并简述作图步骤)(2)取BE中点M,过点M的直线交边AB,CD于点P,Q
题目详情
如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
(1)利用尺规作图补全图形;(要求:保留作图痕迹,并简述作图步骤)
(2)取BE中点M,过点M的直线交边AB,CD于点P,Q.
①当PQ⊥BE时,求证:BP=2AP;
②当PQ=BE时,延长BE,CD交于N点,猜想NQ与MQ的数量关系,并说明理由.

(1)利用尺规作图补全图形;(要求:保留作图痕迹,并简述作图步骤)
(2)取BE中点M,过点M的直线交边AB,CD于点P,Q.
①当PQ⊥BE时,求证:BP=2AP;
②当PQ=BE时,延长BE,CD交于N点,猜想NQ与MQ的数量关系,并说明理由.
▼优质解答
答案和解析
(1)如图1,分别以点B、C为圆心,BC长为半径作弧交正方形内部于点T,连接BT并延长交边AD于点E;
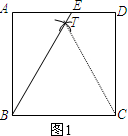
(2)连接PE,如图2,
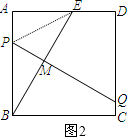
∵点M是BE的中点,PQ⊥BE
∴PQ垂直平分BE.
∴PB=PE,
∴∠PEB=∠PBE=90°-∠AEB=90°-60°=30°,
∴∠APE=∠PBE+∠PEB=60°,
∴∠AEP=90°∠APE=90°-60°=30°,
∴BP=EP=2AP.
(3)NQ=2MQ或NQ=MQ.
理由如下:
如图3所示,过点Q作QF⊥AB于点F交BC于点G,则QF=CB.
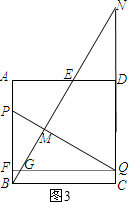
∵正方形ABCD中,AB=BC,
∴FQ=AB.
在Rt△ABE和Rt△FQP中,
∵
∴△ABE≌△FQP(HL).
∴∠FQP=∠ABE=30°.
又∵∠MGO=∠AEB=60°,
∴∠GMO=90°,
∵CD∥AB.
∴∠N=∠ABE=30°.
∴NQ=2MQ.
如图4所示,过点Q作QF⊥AB于点F交BC于点G,则QF=CB.
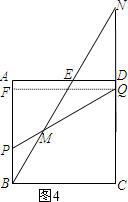
同理可证△ABE≌△FQP.
此时∠FPQ=∠AEB=60°.
又∵∠FPQ=∠ABE+∠PMB,∠N=∠ABE=30°.
∴∠EMQ=∠PMB=30°.
∴∠N=∠EMQ,
∴NQ=MQ.

(2)连接PE,如图2,

∵点M是BE的中点,PQ⊥BE
∴PQ垂直平分BE.
∴PB=PE,
∴∠PEB=∠PBE=90°-∠AEB=90°-60°=30°,
∴∠APE=∠PBE+∠PEB=60°,
∴∠AEP=90°∠APE=90°-60°=30°,
∴BP=EP=2AP.
(3)NQ=2MQ或NQ=MQ.
理由如下:
如图3所示,过点Q作QF⊥AB于点F交BC于点G,则QF=CB.

∵正方形ABCD中,AB=BC,
∴FQ=AB.
在Rt△ABE和Rt△FQP中,
∵
|
∴△ABE≌△FQP(HL).
∴∠FQP=∠ABE=30°.
又∵∠MGO=∠AEB=60°,
∴∠GMO=90°,
∵CD∥AB.
∴∠N=∠ABE=30°.
∴NQ=2MQ.
如图4所示,过点Q作QF⊥AB于点F交BC于点G,则QF=CB.

同理可证△ABE≌△FQP.
此时∠FPQ=∠AEB=60°.
又∵∠FPQ=∠ABE+∠PMB,∠N=∠ABE=30°.
∴∠EMQ=∠PMB=30°.
∴∠N=∠EMQ,
∴NQ=MQ.
看了如图,四边形ABCD为正方形....的网友还看了以下:
4条直线两两相交交,只有1个交点或6个,咋画? 2020-03-30 …
赤道上的特殊时间点比如地球上与晨线的交点是6点……赤道上在什么时候有些什么特殊的时间点 2020-05-14 …
时间和是如何确定的,与日出的关系呢太阳在固定经度上日出日落的“时间”固定吗?还是时间是按照每地的日 2020-07-25 …
在同一平面内不平行的两条直线一定相交.两条直线相交,最多会有1个交点,3条直线相交最多会有3个支点 2020-07-31 …
如图所示,一次函数y=k1x+b与反比例函数y=(x<0)的图象相交于A,B两点,且与坐标轴的交点为 2020-11-01 …
为什么赤道上昼夜平分?为什么赤道与晨昏线的交点为6点、18点?本人愚昧,最好能附上图示, 2020-11-23 …
4条直线两两相交有()个交点,规律是什么? 2020-11-27 …
直线相交的增加规律是什么?比如2条直线相交有一个交点3条直线相交有3个交点4条直线相交有6个交点等等 2020-11-27 …
5条直线有多少交点,规律是什么 2020-11-27 …
读图,回答9~11题.甲点位于北半球某经线与晨线的交点,6月22日甲点正午太阳高度角的范围()A.0 2021-01-23 …