如图1是一个新款水杯，水杯不盛水时按如图2所示的位置放置，这样可以快速晾干杯底，干净透气；将图2的主体部分的抽象成图3，此时杯口与水平直线的夹角为35°，四边形ABCD可以看作矩形

Question

如图1是一个新款水杯，水杯不盛水时按如图2所示的位置放置，这样可以快速晾干杯底，干净透气；将图2的主体部分的抽象成图3，此时杯口与水平直线的夹角为35°，四边形ABCD可以看作矩形，测得AB=10cm，BC=8cm，过点A作AF⊥CE，交CE于点F．
（1）求∠BAF的度数；
（2）求点A到水平直线CE的距离AF的长（精确到0.1cm）
（参考数据sin35°≈0.5736，cos35°≈0.8192，tan35°≈0.7002）

Answer 1

（1）∵四边形ABCD是矩形，
∴∠D=∠BCD=90°，
∴∠DAF=∠DCE=90°-35°=55°，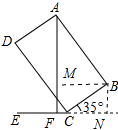
∴∠BAF=90°-55°=35°；
（2）作BM⊥AF于M，BN⊥EF于N，如图所示：
则MF=BN=BC•sin35°=0.5736×8≈4.59（cm），
AM=AB•cos35°=10×0.8192≈8.20，（cm），
∴AF=AM+MF=8.20+4.59≈12.8（cm）；
即A到水平直线CE的距离AF的长为12.8cm．