早教吧作业答案频道 -->数学-->
如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证:△BDF是等腰三角形;(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.①判断四边形BFDG的
题目详情
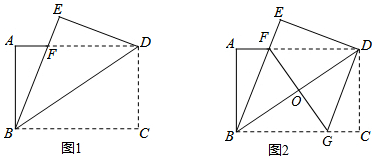
如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.

▼优质解答
答案和解析
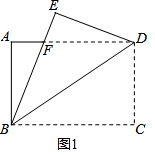 (1)证明:如图1,根据折叠,∠DBC=∠DBE,
(1)证明:如图1,根据折叠,∠DBC=∠DBE,
又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF,
∴△BDF是等腰三角形;
(2)①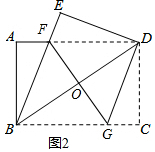 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AD∥BC,
∴FD∥BG,
又∵FD∥BG,
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;
②∵AB=6,AD=8,
∴BD=10.
∴OB=
BD=5.
假设DF=BF=x,∴AF=AD-DF=8-x.
∴在直角△ABF中,AB2+A2=BF2,即62+(8-x)2=x2,
解得x=
,
即BF=
,
∴FO=
=
=
,
∴FG=2FO=
.
 (1)证明:如图1,根据折叠,∠DBC=∠DBE,
(1)证明:如图1,根据折叠,∠DBC=∠DBE,又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF,
∴△BDF是等腰三角形;
(2)①
 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,∴AD∥BC,
∴FD∥BG,
又∵FD∥BG,
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;
②∵AB=6,AD=8,
∴BD=10.
∴OB=
| 1 |
| 2 |
假设DF=BF=x,∴AF=AD-DF=8-x.
∴在直角△ABF中,AB2+A2=BF2,即62+(8-x)2=x2,
解得x=
| 25 |
| 4 |
即BF=
| 25 |
| 4 |
∴FO=
| BF2-OB2 |
(
|
| 15 |
| 4 |
∴FG=2FO=
| 15 |
| 2 |
看了如图1,将一张矩形纸片ABCD...的网友还看了以下:
在DNA分子的碱基组成中,因生物种类不同而异的是A.(A+T)/(G+C) B.C/GC.A/T 2020-04-06 …
如图,写出下列互余与互补的角.已知左图中∠AOC=∠BOD=∠BOE=90°.右图中∠C=∠B=∠ 2020-05-13 …
写出下列自然大调的音阶:G,D,F,降B,降E,A,E,B,降A,降D.好的奖50,快,有赏:写出 2020-05-16 …
结构力学题静定结构内力计算请问上下两幅图的集中力偶为什么表示方式不同,还有上图G、B两处的集中力偶 2020-05-17 …
高一化学!马上要!!1.某温度下,ag饱和硝酸钾溶液蒸干得bg硝酸钾,此温度下,硝酸钾的溶解度计算 2020-06-10 …
设G=为无环的无向图,|V|=6,|E|=16,则G是()A.完全图B.零图C.D.多重图设A和B 2020-06-12 …
实数a,b,c在数轴上的对应点如图所示其中丨a丨=丨c丨,化简丨b-c丨-丨b-a丨+丨a-c-2b 2020-11-01 …
若有以下说明,则数值为4的表达式是().inta[12]={1,2,3,4,5,6,7,8,9,10 2020-12-23 …
如图,在正方形ABCD中,G是BC上的任意一点(G与B,C两点不重合),E,F是AG上的两点(E,F 2021-01-11 …
已知abc为三个有理数,他们的在数轴上对应的位置如图,则|c-b|-|b-a|-|a-c|= 2021-01-16 …