早教吧作业答案频道 -->数学-->
如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△
题目详情
如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E,A′两点.
(1)填空:∠AOB=___°,用m表示点A′的坐标:A′(___,___);
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且
=
时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
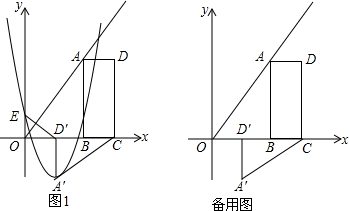
(1)填空:∠AOB=___°,用m表示点A′的坐标:A′(___,___);
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且
| BP |
| AP |
| 1 |
| 3 |
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.

▼优质解答
答案和解析
(1)∵B(2m,0),C(3m,0),
∴OB=2m,OC=3m,即BC=m,
∵AB=2BC,
∴AB=2m=0B,
∵∠ABO=90°,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,
由旋转的性质得:OD′=D′A′=m,即A′(m,-m);
故答案为:45;m,-m;
(2)△D′OE∽△ABC,理由如下:
由已知得:A(2m,2m),B(2m,0),
∵
=
,
∴P(2m,
m),
∵A′为抛物线的顶点,
∴设抛物线解析式为y=a(x-m)2-m,
∵抛物线过点E(0,n),
∴n=a(0-m)2-m,即m=2n,
∴OE:OD′=BC:AB=1:2,
∵∠EOD′=∠ABC=90°,
∴△D′OE∽△ABC;
(3)①当点E与点O重合时,E(0,0),
∵抛物线y=ax2+bx+c过点E,A,
∴
,
整理得:am+b=-1,即b=-1-am;
②∵抛物线与四边形ABCD有公共点,
∴抛物线过点C时的开口最大,过点A时的开口最小,
若抛物线过点C(3m,0),此时MN的最大值为10,
∴a(3m)2-(1+am)•3m=0,
整理得:am=
,即抛物线解析式为y=
x2-
x,
由A(2m,2m),可得直线OA解析式为y=x,
联立抛物线与直线OA解析式得:
,
解得:x=5m,y=5m,即M(5m,5m),
令5m=10,即m=2,
当m=2时,a=
;
若抛物线过点A(2m,2m),则a(2m)2-(1+am)•2m=2m,
解得:am=2,
∵m=2,
∴a=1,
则抛物线与四边形ABCD有公共点时a的范围为
≤a≤1.
∴OB=2m,OC=3m,即BC=m,
∵AB=2BC,
∴AB=2m=0B,
∵∠ABO=90°,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,
由旋转的性质得:OD′=D′A′=m,即A′(m,-m);
故答案为:45;m,-m;
(2)△D′OE∽△ABC,理由如下:
由已知得:A(2m,2m),B(2m,0),
∵
| BP |
| AP |
| 1 |
| 3 |
∴P(2m,
| 1 |
| 2 |
∵A′为抛物线的顶点,
∴设抛物线解析式为y=a(x-m)2-m,
∵抛物线过点E(0,n),
∴n=a(0-m)2-m,即m=2n,
∴OE:OD′=BC:AB=1:2,
∵∠EOD′=∠ABC=90°,
∴△D′OE∽△ABC;
(3)①当点E与点O重合时,E(0,0),
∵抛物线y=ax2+bx+c过点E,A,
∴
|
整理得:am+b=-1,即b=-1-am;
②∵抛物线与四边形ABCD有公共点,
∴抛物线过点C时的开口最大,过点A时的开口最小,
若抛物线过点C(3m,0),此时MN的最大值为10,
∴a(3m)2-(1+am)•3m=0,
整理得:am=
| 1 |
| 2 |
| 1 |
| 2m |
| 3 |
| 2 |
由A(2m,2m),可得直线OA解析式为y=x,
联立抛物线与直线OA解析式得:
|
解得:x=5m,y=5m,即M(5m,5m),
令5m=10,即m=2,
当m=2时,a=
| 1 |
| 4 |
若抛物线过点A(2m,2m),则a(2m)2-(1+am)•2m=2m,
解得:am=2,
∵m=2,
∴a=1,
则抛物线与四边形ABCD有公共点时a的范围为
| 1 |
| 4 |
看了如图1,B(2m,0),C(3...的网友还看了以下:
范成大《喜晴》后两句连雨不知春去,一晴方觉夏深.点评一下,不要光说意思,要点评!点评点评点评点评点 2020-04-27 …
已知椭圆的中心在原点,焦点在x轴,从焦点看短轴的两个端点.已知椭圆的中心在原点,焦点在x轴,从焦点 2020-05-16 …
已知边长为4的等边三角形ABC,顶点B在坐标原点,顶点C在X轴正半轴上,顶点A在X轴上方.现将△A 2020-05-16 …
如图,在平面直角坐标系中,直线y=4/3x+4与x轴交于点A,与y轴交于点B,点C为y轴上一动点( 2020-05-16 …
抛物线Y=-X²+2X+3与X轴相交于点A,B两点(点A在点B左侧),与Y轴交于点C,顶点为D.连 2020-06-02 …
已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、 2020-06-18 …
已知O为坐标原点,点F的坐标为(1,0),点P是直线m:x=-1上一动点,点M为PF的中点,点Q满 2020-08-02 …
已知△ABC中,角C=90度,AB=9,cosA=2/3,把△ABC绕着点C旋转,使得点A落在点D, 2020-11-02 …
时间的问题,把括号填写完整子时(夜半):23点到1点.()时(鸡鸣):1点到()点.寅时(平旦):( 2020-12-01 …
如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB、CB边上的动点,点P与点Q同时出 2020-12-03 …