早教吧作业答案频道 -->数学-->
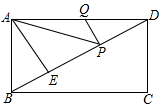
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为.
题目详情
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为___.

▼优质解答
答案和解析
设BE=x,则DE=3x,
∵四边形ABCD为矩形,且AE⊥BD,
∴△ABE∽△DAE,
∴AE2=BE•DE,即AE2=3x2,
∴AE=
x,
在Rt△ADE中,由勾股定理可得AD2=AE2+DE2,即62=(
x)2+(3x)2,解得x=
,
∴AE=3,DE=3
,
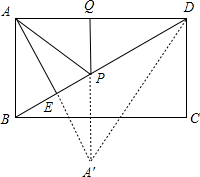
如图,设A点关于BD的对称点为A′,连接A′D,PA′,
则A′A=2AE=6=AD,AD=A′D=6,
∴△AA′D是等边三角形,
∵PA=PA′,
∴当A′、P、Q三点在一条线上时,A′P+PQ最小,
又垂线段最短可知当PQ⊥AD时,A′P+PQ最小,
∴AP+PQ=A′P+PQ=A′Q=DE=3
.
故答案是:3
.

设BE=x,则DE=3x,
∵四边形ABCD为矩形,且AE⊥BD,
∴△ABE∽△DAE,
∴AE2=BE•DE,即AE2=3x2,
∴AE=
| 3 |
在Rt△ADE中,由勾股定理可得AD2=AE2+DE2,即62=(
| 3 |
| 3 |
∴AE=3,DE=3
| 3 |
如图,设A点关于BD的对称点为A′,连接A′D,PA′,
则A′A=2AE=6=AD,AD=A′D=6,
∴△AA′D是等边三角形,
∵PA=PA′,
∴当A′、P、Q三点在一条线上时,A′P+PQ最小,
又垂线段最短可知当PQ⊥AD时,A′P+PQ最小,
∴AP+PQ=A′P+PQ=A′Q=DE=3
| 3 |
故答案是:3
| 3 |
看了如图,在矩形ABCD中,AD=...的网友还看了以下:
正方体ABCD-A’B"C"D"中P,Q,R分别是AB,AD,BC的中点,那么正方体的过P,Q,R 2020-05-13 …
漂白粉长期暴露在空气中变质的原因是A.漂白粉在空气中潮解了B.漂白粉分解了C.漂白粉中的氯化钙吸收 2020-05-17 …
如图,在△ABC中,D是BC的重点,DE垂直AB,DF垂直AC,垂直分别是D,F,BE=CF,求证 2020-05-21 …
二重积分的计算问题计算∫∫(x^2*y^2)dσ,其中D是由xy=2,xy=4,y=x,y=3x在 2020-06-05 …
计算二重积分arctgy/xdxdy,其中D={(x,y)|1≤x^2+y^2≤4,0≤y≤x}计 2020-06-10 …
在容积相同的不同密闭容器内,分别充入同量的N2和H2,在不同温度,任其发生反应N2+3H2⇌2NH 2020-06-23 …
请帮我解决这三条题啦!计算二重积分:1、∫∫[D](y^2/x^2)dxdy,其中D由y=x,y= 2020-06-26 …
图示体液免疫过程,请分析回答有关问题:(1)图中D为 细胞,由图示体液免疫过程,请分析回答有关问题 2020-06-27 …
(12分)已知细胞合成DNA有D和S两条途径,其中D途径能被氨基嘌呤阻断。人淋巴细胞中有这两种DN 2020-07-02 …
已知细胞合成DNA有D和S两条途径,其中D途径能被氨基嘌呤阻断,人淋巴细胞中有这两种DNA的合成途 2020-07-02 …