早教吧作业答案频道 -->数学-->
如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.(1)求证:DE∥BC;(2)求证:DE=12(BC-AB);(3)若∠ABC=72°,求∠ADE的度数.
题目详情
如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.
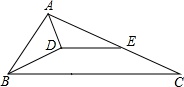
(1)求证:DE∥BC;
(2)求证:DE=
(BC-AB);
(3)若∠ABC=72°,求∠ADE的度数.

(1)求证:DE∥BC;
(2)求证:DE=
| 1 |
| 2 |
(3)若∠ABC=72°,求∠ADE的度数.
▼优质解答
答案和解析
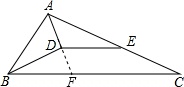 (1)证明:如图,延长AD交BC于F,
(1)证明:如图,延长AD交BC于F,
∵BD平分∠ABC,AD⊥BD,
∴AB=BF,AD=DF,
又∵E为AC的中点,
∴DE是△ACF的中位线,
∴DE∥BC;
(2)证明:∵AB=BF,
∴FC=BC-AB,
∵DE是△ACF的中位线,
∴DE=
(BC-AB);
(3) ∵∠ABC=72°,
∴∠AFB=
(180°-72°)=54°,
∵DE∥BC,
∴∠ADE=∠AFB=54°.
 (1)证明:如图,延长AD交BC于F,
(1)证明:如图,延长AD交BC于F,∵BD平分∠ABC,AD⊥BD,
∴AB=BF,AD=DF,
又∵E为AC的中点,
∴DE是△ACF的中位线,
∴DE∥BC;
(2)证明:∵AB=BF,
∴FC=BC-AB,
∵DE是△ACF的中位线,
∴DE=
| 1 |
| 2 |
(3) ∵∠ABC=72°,
∴∠AFB=
| 1 |
| 2 |
∵DE∥BC,
∴∠ADE=∠AFB=54°.
看了如图,△ABC中,BD平分∠A...的网友还看了以下:
某次考试A、B、C、D、E五人的成绩统计如下:A、B、C、D的平均分是75分;A、C、D、E的平均分 2020-03-31 …
将△ABD平移,使D沿BD延长线至C得到A′B′D′,A′B′交于AC于E,AD平行∠BAC.1. 2020-05-19 …
在一次考试中,A、B、C、D四人的得分是不小于90且互不相同的整数,四人的平均分也是整数,A、B、 2020-05-20 …
某次考试,A.B.C.D四人的成绩如下:A.B.C平均分:91分B.C.D平均分:89分A.D平均 2020-05-20 …
在一次考试中,A、B、C、D四人的得分是不小于90且互不相同的整数,四人的平均分也是整数,A、B、 2020-05-21 …
在一次考试中,A,B,C,D四人的得分是不小于90且互不相同的整数,四人的平均分也是整数,A,B, 2020-05-21 …
已知b分之a=d分之c=f分之e=2且b+d+f≠0.(1)b+d+f分之a+c+e=(2)b-d 2020-06-09 …
分子分母比例相同的两个分数,让它们分子减分子,分母减分母,得到的比例还一样吗,这个定理叫什么名字? 2020-07-18 …
高数题目一、单选题(共10道试题,共60分。)题面见图片A.B.C.D.满分:6分2.题面见图片A. 2020-11-01 …
D是一中蓝色溶液,可配置波尔多液,A、B、C、E分别是单质、酸、碱、盐A分别能与B和D反应,C分别能 2020-12-26 …