早教吧作业答案频道 -->数学-->
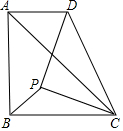
如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为.
题目详情
如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为___.

▼优质解答
答案和解析
如图,作PF⊥BC于点F,延长FP交AD于点E,
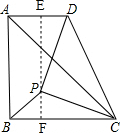
∵AD∥BC,
∴∠PFC=∠DEP=90°,
∴∠CPF+∠PCF=90°,
∵∠DPC=90°,
∴∠CPF+∠DPE=90°,
∴∠PCF=∠DPE,
在△PCF和△DPE中,
∵
,
∴△PCF≌△DPE(AAS),
∴PF=DE、PE=CF,
设PF=DE=x,则PE=CF=4-x,
∵S四边形ABCD=
(AD+BC)•AB=12,
∴
×(AD+4)×4=12,解得AD=2,
∴AE=BF=2-x,
∴FC=BC-BF=4-(2-x)=2+x,
可得2+x=4-x,解得x=1,
∴BP=
=
,
故答案为:
.

∵AD∥BC,
∴∠PFC=∠DEP=90°,
∴∠CPF+∠PCF=90°,
∵∠DPC=90°,
∴∠CPF+∠DPE=90°,
∴∠PCF=∠DPE,
在△PCF和△DPE中,
∵
|
∴△PCF≌△DPE(AAS),
∴PF=DE、PE=CF,
设PF=DE=x,则PE=CF=4-x,
∵S四边形ABCD=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴AE=BF=2-x,
∴FC=BC-BF=4-(2-x)=2+x,
可得2+x=4-x,解得x=1,
∴BP=
| BF2+PF2 |
| 2 |
故答案为:
| 2 |
看了如图,在等腰Rt△ABC中,∠...的网友还看了以下:
从上底的一点到下底引一条垂线,这点和垂足之间的线段叫做梯形的()A.腰B.垂线C.高 2020-03-31 …
26.(14分)已知A、B、C、D、E是核电荷数依次增大的不同主族的短周期元素,A、B形成的一种化 2020-04-08 …
如图表示酶催化反应过程的示意图,下列叙述错误的是()A.图中b表示二肽B.图中a与b结合后,a的形 2020-05-14 …
在梯形中,互相平行的一组对边叫做梯形的()A.腰B.上底和下底C.高 2020-05-20 …
A与C同主族元素,在A与B形成的化合物种,A的质量分数为2/5,在A与C形成的化合物中,A的质量分 2020-06-05 …
高速旋转机械的转子轴颈磨损后,圆柱度误差常出现( )。A.腰鼓形B.马鞍形C.锥形 2020-06-07 …
短周期主族元素A、B形成AB3型分子,下列有关叙述正确的是()A.若A、B为同一周期元素,则AB3 2020-06-17 …
已知A、B、C、D、E是原子序数依次增大的五种短周期元素,A与C同主族,A与B、A与E形成共价化合物 2020-11-01 …
a元素原子的核电荷数为11,b元素的核内质子数为8,A和B形成化合物Z,下列说法中错误的是()A.A 2020-11-18 …
在梯形中,互相平行的一组对边叫做梯形的()A.腰B.上底和下底C.高 2020-12-01 …