早教吧作业答案频道 -->数学-->
已知正方形ABCD的边长为5,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.(1)当点E在边CB的延长线上,点M在边AD上时,如图1,求证:BE+AM=AB;(2)当点E
题目详情
已知正方形ABCD的边长为5,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.
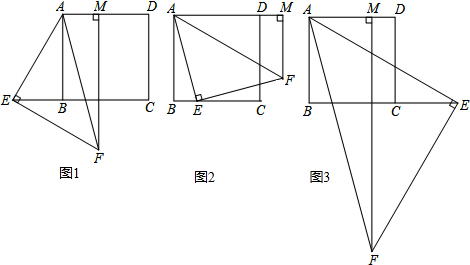
(1)当点E在边CB的延长线上,点M在边AD上时,如图1,求证:BE+AM=AB;
(2)当点E在边BC上,点M在边AD的延长线上时,如图2,设BE=x,AM=y,求y关于x的函数关系式,并写出函数定义域;
(3)当点E在边BC的延长线上,点M在边AD上时,如图3.如果∠AFM=15°,求AM的长.

(1)当点E在边CB的延长线上,点M在边AD上时,如图1,求证:BE+AM=AB;
(2)当点E在边BC上,点M在边AD的延长线上时,如图2,设BE=x,AM=y,求y关于x的函数关系式,并写出函数定义域;
(3)当点E在边BC的延长线上,点M在边AD上时,如图3.如果∠AFM=15°,求AM的长.
▼优质解答
答案和解析
(1)证明:设FM交边BC于点N,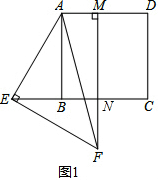
∵四边形ABCD是正方形,
∴∠ABC=90°,AD∥BC,
∴∠ABE=90°,
∴∠BAE+∠AEB=90°
∵△AEF是等腰直角三角形,
∴∠AEF=90°,AE=EF,
∴∠NEF+∠AEB=90°,
∴∠BAE=∠NEF
∵FM⊥AD,
∴FM⊥BC,
∴∠ENF=90°,
∴∠ABE=∠ENF,
在△ABE和△ENF中,
,
∴△ABE≌△ENF
∴AB=EN,
∵∠ABC=∠BNM=∠NMA=90°,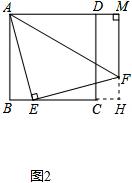
∴四边形ABNM是矩形,
∴AM=BN,
∵EN=BE+BN,
∴AB=BE+AM;
(2)延长MF交BC的延长线于点H,由(1)得AB=EH=5,
∵∠MAB=∠ABH=∠AMH=90°,
∴四边形ABHM是矩形,
∴AM=BH=y,
∵BH=BE+EH,BE=x,
∴y=x+5(0<x<5);
(3)设FM交边BC于点G,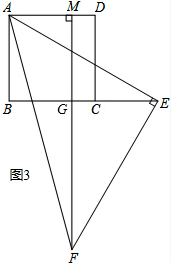
∵△AEF是等腰直角三角形,
∴∠AFE=45°,
∵∠AFM=15°,
∴∠EFG=30°,
∴∠AEB=∠EFG=30°,
在Rt△ABE中,AB=5,∠AEB=30°,
∴AE=10,BE=5
5
,
∵△ABE≌△EGF,
∴AB=EG=5
∴BG=5
-55
-5,
∵∠MAB=∠ABC=∠GMA=90°
∴四边形ABGM是矩形,
∴AM=BG,
∴AM=5
-55
-5.

∵四边形ABCD是正方形,
∴∠ABC=90°,AD∥BC,
∴∠ABE=90°,
∴∠BAE+∠AEB=90°
∵△AEF是等腰直角三角形,
∴∠AEF=90°,AE=EF,
∴∠NEF+∠AEB=90°,
∴∠BAE=∠NEF
∵FM⊥AD,
∴FM⊥BC,
∴∠ENF=90°,
∴∠ABE=∠ENF,
在△ABE和△ENF中,
|
∴△ABE≌△ENF
∴AB=EN,
∵∠ABC=∠BNM=∠NMA=90°,

∴四边形ABNM是矩形,
∴AM=BN,
∵EN=BE+BN,
∴AB=BE+AM;
(2)延长MF交BC的延长线于点H,由(1)得AB=EH=5,
∵∠MAB=∠ABH=∠AMH=90°,
∴四边形ABHM是矩形,
∴AM=BH=y,
∵BH=BE+EH,BE=x,
∴y=x+5(0<x<5);
(3)设FM交边BC于点G,

∵△AEF是等腰直角三角形,
∴∠AFE=45°,
∵∠AFM=15°,
∴∠EFG=30°,
∴∠AEB=∠EFG=30°,
在Rt△ABE中,AB=5,∠AEB=30°,
∴AE=10,BE=5
| 3 |
| 3 |
∵△ABE≌△EGF,
∴AB=EG=5
∴BG=5
| 3 |
| 3 |
∵∠MAB=∠ABC=∠GMA=90°
∴四边形ABGM是矩形,
∴AM=BG,
∴AM=5
| 3 |
| 3 |
看了已知正方形ABCD的边长为5,...的网友还看了以下:
1.a+a的-1此方=3a的平方+a的-2此方=?2.已知三角形ABC为等边三角形,D是BC上一点 2020-04-26 …
三角形已知平行四边形abcd,ab边上一点e,bc上一点f,三角形ade的面积5,三角形bef面已 2020-05-17 …
已知三角形ABC,AD是角BC边上的中线,分别以AB边、AC边为直角边各向形外做等腰直角三角形.求 2020-07-09 …
凸四边形公式证明已知凸四边形四边长分别为a,b,c,d,对角线长度分别为e,f,对角线中点的连线长 2020-07-25 …
如果凸n边形F(n≥4)的所有对角线都相等,那么A.F∈{四边形}B.F∈{五边形}C.F∈{四边 2020-07-25 …
已知过一个凸多边形的不相邻的两个端点的连线段称为该凸多边形的对角线.(Ⅰ)分别求出凸四边形,凸五边 2020-08-01 …
三角形内接平行四边形已知,平行四边形内接于三角形ABC,D是线段AB上一点,G、F是三角形底边BC 2020-08-03 …
初二数学题,在线等,多谢.已知,如图,三角形ABC中,角ACB等于90度,角BAC等于30度,分别以 2020-11-03 …
已知:如图,在三角形ABC中,角ACB=90度,以AB为边在三角形ABC外作三角形ABD,角ADB= 2020-11-03 …
七下期末统考卷几何题如图,已知角BAC=50度,两块三角板如图摆放,点B和C分别在两块三角板的边上, 2020-11-06 …