早教吧作业答案频道 -->数学-->
(1)阅读并填空:如图①,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.试说明∠D=90°+12∠A的理由.因为BD平分∠ABC(已知),所以∠1=(角平分线定义).同理:
题目详情
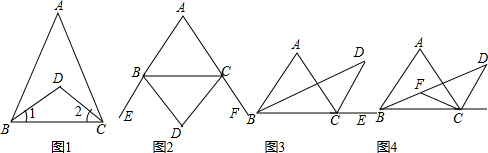
(1)阅读并填空:如图①,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.
试说明∠D=90°+
∠A的理由.
因为BD平分∠ABC(已知),
所以∠1=___(角平分线定义).
同理:∠2=___.
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,(___),
所以___(等式性质).
即:∠D=90°+
∠A.
(2)探究,请直接写出结果,无需说理过程:
(i)如图②,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是___.
(ii)如图③,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是___.
(3)如图④,△ABC中,∠A=90°,BF、CF分别平分∠ABC、∠ACB,CD是△ABC的外角∠ACE的平分线.试说明DC=CF的理由.
试说明∠D=90°+
| 1 |
| 2 |
因为BD平分∠ABC(已知),
所以∠1=___(角平分线定义).
同理:∠2=___.
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,(___),
所以___(等式性质).
即:∠D=90°+
| 1 |
| 2 |
(2)探究,请直接写出结果,无需说理过程:
(i)如图②,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是___.
(ii)如图③,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是___.
(3)如图④,△ABC中,∠A=90°,BF、CF分别平分∠ABC、∠ACB,CD是△ABC的外角∠ACE的平分线.试说明DC=CF的理由.

▼优质解答
答案和解析
(1) 因为BD平分∠ABC(已知),
所以∠1=
∠ABC (角平分线定义).
同理:∠2=
∠ACB.
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°(三角形的内角和等于180°),
所以∠D=180°-(∠1+∠2)=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)=90°+
∠A(等式性质).
即:∠D=90°+
∠A.
(2) (i)∠D与∠A之间的等量关系是:∠D=90°-
∠A.
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°-2∠DBC,
∠ACB=180°-2∠DCB,
∴∠A+180°-2∠DBC+180°-2∠DCB=180°,
∴∠A-2(∠DBC+∠DCB)=-180°,
∴∠A-2(180°-∠D)=-180°,
∴∠A-2∠D=180°,
∴∠D=90°-
∠A
(ii)∠D与∠A之间的等量关系是:∠D=
∠A.
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D,
∵∠A+2∠DBC=2∠DCE
∴∠A+2∠DBC=2∠DBC+2∠D
∴∠A=2∠D
即:∠D=
∠A
(3) 因为 BD平分∠ABC(已知),
所以∠DBC=
∠ABC(角平分线定义).
同理:∠ACF=
∠ACB,∠DCA=∠DCE=
∠ACE.
∵∠ACE=∠ABC+∠A,∠DCE=∠DBC+∠D(三角形的一个外角
等于两个不相邻的内角和),
∴∠D=∠DCE-∠DBC=
(∠ACE-∠ABC)=
∠A.
又∵∠A=90°(已知),
∴∠D=45°(等式性质).
∵∠ACB+∠ACE=180°(平角的定义),
∴∠FCD=∠FCA+∠ACD=
(∠BCA+∠ACE)=90°.
∵∠D+∠DFC+∠FCD=180°(三角形的内角和等于180°),
∴∠DFC=45°(等式性质).
∴∠D=∠DFC(等量代换).
∴DC=FC.(等角对等边).
所以∠1=
| 1 |
| 2 |
同理:∠2=
| 1 |
| 2 |
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°(三角形的内角和等于180°),
所以∠D=180°-(∠1+∠2)=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
| 1 |
| 2 |
即:∠D=90°+
| 1 |
| 2 |
(2) (i)∠D与∠A之间的等量关系是:∠D=90°-
| 1 |
| 2 |
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°-2∠DBC,
∠ACB=180°-2∠DCB,
∴∠A+180°-2∠DBC+180°-2∠DCB=180°,
∴∠A-2(∠DBC+∠DCB)=-180°,
∴∠A-2(180°-∠D)=-180°,
∴∠A-2∠D=180°,
∴∠D=90°-
| 1 |
| 2 |
(ii)∠D与∠A之间的等量关系是:∠D=
| 1 |
| 2 |
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D,
∵∠A+2∠DBC=2∠DCE
∴∠A+2∠DBC=2∠DBC+2∠D
∴∠A=2∠D
即:∠D=
| 1 |
| 2 |
(3) 因为 BD平分∠ABC(已知),
所以∠DBC=
| 1 |
| 2 |
同理:∠ACF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACE=∠ABC+∠A,∠DCE=∠DBC+∠D(三角形的一个外角
等于两个不相邻的内角和),
∴∠D=∠DCE-∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠A=90°(已知),
∴∠D=45°(等式性质).
∵∠ACB+∠ACE=180°(平角的定义),
∴∠FCD=∠FCA+∠ACD=
| 1 |
| 2 |
∵∠D+∠DFC+∠FCD=180°(三角形的内角和等于180°),
∴∠DFC=45°(等式性质).
∴∠D=∠DFC(等量代换).
∴DC=FC.(等角对等边).
看了(1)阅读并填空:如图①,BD...的网友还看了以下:
判断下列画线部分发音是否相同,相同的“t”不同的“f"()1.isit画线部分i()2.stude 2020-05-14 …
选出下列各组中画线部分读音不同的单词()1.Aplay画线部分:pl.Bprice画线部分:pr. 2020-05-14 …
划线部分发音相同的打√,不同的打×()1.facecake(划线部分是a)()2.openoran 2020-05-17 …
一个长方形上画线,一条线最多能分2部分,两条线最多可以分4部分,3条线最多分4部分,那么N条线能分 2020-05-20 …
选出下列各组单词画线部分读音不同的选项.()1.A.thank(画线部分:a)B.am(画线部分: 2020-05-23 …
单词辨音,判断每组单词划线部分的读音是(S)否(D)相同1.milk(划线部分为i)this(划线 2020-05-24 …
判断下列单词画线部分是否相同,相同打钩,不相同打叉.paperher画线部分是erbottleho 2020-07-08 …
先将线段AB分成20等分,线段上的等分点用“△”标注……[要原理]急~先将线段AB分成20等分,线 2020-08-02 …
就画线部分提问todayiswednesday(划线部分是wednesday)mybrotheri 2020-08-03 …
日K线图里面有五条线,其中分别是白线,黄线,紫线,绿线;分别是5日,10日,20日,30日,60日均 2020-12-05 …