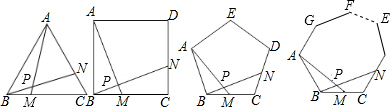
小睿同学在探究性课题的研究中发现了正多边形的一个规律：下面四个图分别是正三角形ABC、正方形ABCD、正五边形ABCDE和正n边形ABCDE…F，点M、N分别是相邻两条边上的点且满足BM=CN，连接AM、

Question

小睿同学在探究性课题的研究中发现了正多边形的一个规律：下面四个图分别是正三角形ABC、正方形ABCD、正五边形ABCDE和正n边形ABCDE…F，点M、N分别是相邻两条边上的点且满足BM=CN，连接AM、BN，相交于点P，小睿通过证明△ABM和△BCN全等，分别得到了在正三角形ABC中，∠APN=60°；在正方形ABCD中，∠APN=90°，在正五边形ABCDE中，∠APN=108°，请沿着小睿的思路，尝试计算在正n边形ABCDE…F中，∠APN=___°（用含有n的代数式表示）

Answer 1

结论：∠APN=((n-2)180°)/(n)．
理由：在△ABM和△BCN中，

AB=BC

∠ABM=∠BCN

BM=CN

，
∴△ABM≌△BCN．
∴∠BAM=∠CBN．
∴∠APN=∠BAM+∠ABN=∠CBN+∠ABN=∠ABC=((n-2)180°)/(n)．
故答案为((n-2)180°)/(n)．