早教吧作业答案频道 -->数学-->
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=22,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.(Ⅰ)证明:平面AB1C⊥平面BCD;(Ⅱ)若G为B1C上的一点,A1G∥平面BCD,证明:G为B1C的中
题目详情
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2
,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.
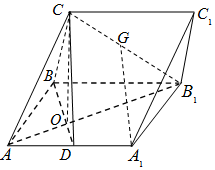
(Ⅰ)证明:平面AB1C⊥平面BCD;
(Ⅱ)若G为B1C上的一点,A1G∥平面BCD,证明:G为B1C的中点.
| 2 |

(Ⅰ)证明:平面AB1C⊥平面BCD;
(Ⅱ)若G为B1C上的一点,A1G∥平面BCD,证明:G为B1C的中点.
▼优质解答
答案和解析
(本小题满分12分)
证明:(Ⅰ)∵ABB1A1为矩形,AB=2,AA1=2
,D是AA1的中点,
∴∠BAD=90°,∠ABB1=900,BB1=2
,AD=
AA1=
从而△ABD∽△ABB1,
∴∠ABD=∠AB1B…(2分)
∴∠AB1B+∠BAB1=∠ABD+∠BAB1=
,∴∠AOB=
,从而AB1⊥BD…(4分)
∵OC⊥平面ABB1A1,AB1⊂平面ABB1A1,∴AB1⊥OC,
∵BD∩OC=O,∴AB1⊥平面BCD,
∵AB1⊂平面AB1C,∴平面AB1C⊥平面BCD…(6分)
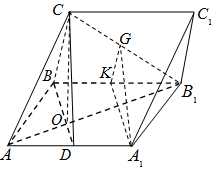
(Ⅱ) 作A1K∥BD交BB1于K,连结KG,
∵A1K⊄平面BCD,BD⊂平面BCD,∴A1K∥平面BCD,
又A1G∥平面BCD,A1K∩A1G=A1
∴平面A1KG∥平面BCD,…(8分)
∵平面BB1C∩平面BCD=BC,平面BB1C∩平面A1KG=KG,∴BC∥KG…(10分)
在矩形ABB1A1中,∵AA1∥BB1,AA1=BB1
∴A1KBD为平行四边形,
从而BK=A1D=
AA1=
BB1,∴K为BB1的中点,
∴G为B1C的中点.…(12分)
证明:(Ⅰ)∵ABB1A1为矩形,AB=2,AA1=2
| 2 |
∴∠BAD=90°,∠ABB1=900,BB1=2
| 2 |
| 1 |
| 2 |
| 2 |
从而△ABD∽△ABB1,

∴∠ABD=∠AB1B…(2分)
∴∠AB1B+∠BAB1=∠ABD+∠BAB1=
| π |
| 2 |
| π |
| 2 |
∵OC⊥平面ABB1A1,AB1⊂平面ABB1A1,∴AB1⊥OC,
∵BD∩OC=O,∴AB1⊥平面BCD,
∵AB1⊂平面AB1C,∴平面AB1C⊥平面BCD…(6分)
(Ⅱ) 作A1K∥BD交BB1于K,连结KG,
∵A1K⊄平面BCD,BD⊂平面BCD,∴A1K∥平面BCD,
又A1G∥平面BCD,A1K∩A1G=A1
∴平面A1KG∥平面BCD,…(8分)
∵平面BB1C∩平面BCD=BC,平面BB1C∩平面A1KG=KG,∴BC∥KG…(10分)
在矩形ABB1A1中,∵AA1∥BB1,AA1=BB1
∴A1KBD为平行四边形,
从而BK=A1D=
| 1 |
| 2 |
| 1 |
| 2 |
∴G为B1C的中点.…(12分)
看了在三棱柱ABC-A1B1C1中...的网友还看了以下:
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1 2020-03-31 …
已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE=FC1= 2020-05-16 …
已知E,F分别是正方体ABCD-A1B1C1D1的棱AA1和棱CC1上的点,且AE=C1F.求证: 2020-05-16 …
下列叙述中正确的是()A.形态解剖学和胚胎学为生物进化提供了直接的证据B.白细胞能穿过毛细血管壁, 2020-05-17 …
全陪在上团前的物质准备主要包括( )。A.必带的证件 B.必带的书籍等有关资料C.所需结算 2020-05-19 …
全陪在上团前的物质准备主要包括( )。 A.必带的证件B.必带的书籍等有关资料C.所需结 2020-05-19 …
全陪在上团前的物质准备主要包括(A.必带的证件B.必带的书籍等有关资料C.所需结算单据和费用D.旅 2020-05-20 …
保险公司委托从事保险销售的人员需要具备的条件是( )。A、持有保险销售人员资格的证明B、持有其 2020-05-22 …
内部审计师工作底稿的主要目的是( )。A.提供审计程序计划和实施情况的证据B.作为编制财务报表的一 2020-05-27 …
内控评价计分的主要依据是()。A.现场测试所获得的证据B.非现场测试所获得证据C.非现场测试和现场 2020-05-27 …