早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.(1)求证:△ADP∽△ABE;(2)若AD:AB=2:3,且CP=2DP,求AF:FB的值.
题目详情
如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.
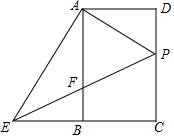
(1)求证:△ADP∽△ABE;
(2)若AD:AB=2:3,且CP=2DP,求AF:FB的值.

(1)求证:△ADP∽△ABE;
(2)若AD:AB=2:3,且CP=2DP,求AF:FB的值.
▼优质解答
答案和解析
(1)证明: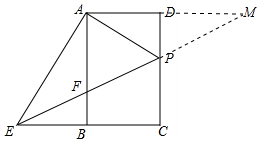 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠ABC=∠BAD=∠ADC=∠ABE=90°,
∵∠EAP=∠BAD=90°,
∴∠EAB=∠PAD,∵∠ABE=∠ADP,
∴△ADP∽△ABE.
(2) 如图,延长AD、EP交于点M.
∵AD:AB=2:3,且CP=2DP,
∴可以假设AD=4a,CD=6a,则PC=4a,DP=2a,
∵△ADP∽△ABE,
∴
=
,
∴
=
,
∴EB=3a,
∵DM∥EC,
∴
=
,
∴
=
,
∴DM=
a,AM=
a,
∵AM∥EB,
∴
=
=
=
.
 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,∴∠ABC=∠BAD=∠ADC=∠ABE=90°,
∵∠EAP=∠BAD=90°,
∴∠EAB=∠PAD,∵∠ABE=∠ADP,
∴△ADP∽△ABE.
(2) 如图,延长AD、EP交于点M.
∵AD:AB=2:3,且CP=2DP,
∴可以假设AD=4a,CD=6a,则PC=4a,DP=2a,
∵△ADP∽△ABE,
∴
| AD |
| AB |
| DP |
| EB |
∴
| 4a |
| 6a |
| 2a |
| EB |
∴EB=3a,
∵DM∥EC,
∴
| DM |
| EC |
| DP |
| PC |
∴
| DM |
| 7a |
| 2a |
| 4a |
∴DM=
| 7 |
| 2 |
| 15 |
| 2 |
∵AM∥EB,
∴
| AF |
| FB |
| AM |
| EB |
| ||
| 3a |
| 5 |
| 2 |
看了如图,在矩形ABCD中,点P在...的网友还看了以下:
概率题急求解1设A,B为随机事件且P(A)=0.7,P(A-B)=0.3,求P(A非B非).2设A 2020-04-12 …
如图所示,沿直线匀速行驶的火车车厢的天花板下竖直悬挂着一个小球,在小球的正下方有一点P,若剪断绳子 2020-05-13 …
已知,PAB为圆的割线,交圆于A、B两点,PC切圆于C点,角CPB的平分先交AC与点E(A点在P、 2020-05-20 …
下列关于企业重视和加强技术创新,培育自主创新能力,说法正确的有:A.是价值规律的内在要求B.是因 2020-05-31 …
设P(A)=a,P(B)=b.如果AB不相容,求P(AUB)=如果AB相互独立.求P(AUB)=如 2020-06-12 …
圆环状合金圈的A点固定接在电路中,滑动触头P可以在圆环上滑动,闭合开关S后,在P从B开始经C滑动到 2020-06-16 …
如图所示,用单色光A做双缝干涉实验时,P处为第二条暗纹的中心,改用频率较低的单色光B重做实验,若其 2020-06-21 …
数轴上两点A,B对应的书分别为-1,4,点p为数轴上一动点,其对应的数为x若点p到点a,点b的距离 2020-06-26 …
.与时俱进是马克思主义的理论品质,这是因为它是A.马克思主义自身的内在要求B.马克思主义的鲜明特色 2020-06-30 …
打点器求瞬时速度的问题有ABC三个点在最小刻度为1mm的直尺上现在让求B点的瞬时速度我现在找到了离 2020-08-02 …