早教吧作业答案频道 -->数学-->
如图,长方形OABC的顶点A、C、O都在坐标轴上,点B的坐标为(9,4),E为BC边上一点,CE=6.(1)求点E的坐标和△ABE的周长;(2)若P是OA上的一个动点,它以每秒1个单位长度的速度从点O出
题目详情
如图,长方形OABC的顶点A、C、O都在坐标轴上,点B的坐标为(9,4),E为BC边上一点,CE=6.
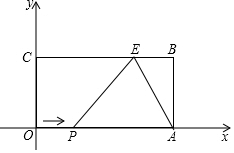
(1)求点E的坐标和△ABE的周长;
(2)若P是OA上的一个动点,它以每秒1个单位长度的速度从点O出发沿射线OA运动,设点P运动的时间为t秒(t>0).
①当t为何值时,△PAE的面积等于△PCE的面积的一半;
②当t为何值时,△PAE为直角三角形.

(1)求点E的坐标和△ABE的周长;
(2)若P是OA上的一个动点,它以每秒1个单位长度的速度从点O出发沿射线OA运动,设点P运动的时间为t秒(t>0).
①当t为何值时,△PAE的面积等于△PCE的面积的一半;
②当t为何值时,△PAE为直角三角形.
▼优质解答
答案和解析
 (1)如图,∵长方形OABC中,点B的坐标为(9,4),
(1)如图,∵长方形OABC中,点B的坐标为(9,4),
∴CB=9,CO=4=AB,
又∵CE=6,
∴E(6,4),BE=3,
∵∠B=90°,
∴Rt△ABE中,AE=
=5,
∴△ABE的周长:3+4+5=12;
(2)①∵OP=1×t=t,
∴AP=9-t,
∵△PAE的面积等于△PCE的面积的一半,
∴当P在OA之间时,
根据
×AP×AB=
×CE×CO×
,可得
(9-t)×4=6×4×
,
解得t=6;
当P在OA的延长线上时,
根据
×AP×AB=
×CE×CO×
,可得
(t-9)×4=6×4×
,
解得t=12;
综上所述,当t为6或12秒时,△PAE的面积等于△PCE的面积的一半;
②如图,当∠PEA=90°时,△PAE为直角三角形,过点P作PF⊥BC于F,则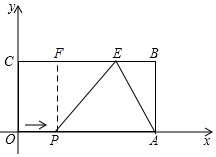
CF=OP=t,EF=6-t,BF=6-t+3=9-t=AP,
由勾股定理可得,PE2+AE2=AP2,
即(PF2+EF2)+AE2=AP2,
∴42+(6-t)2+52=(9-t)2,
解得t=
;
当∠EPA=90°时,△PAE为直角三角形,EP⊥OA,
此时,PE=OC=4,
∴Rt△APE中,AP=
=3,
∴OP=9-3=6,
∴t=6;
∵EA与AP不垂直,
∴∠PAE不可能为直角;
综上所述,当t为6或
秒时,△PAE为直角三角形.
 (1)如图,∵长方形OABC中,点B的坐标为(9,4),
(1)如图,∵长方形OABC中,点B的坐标为(9,4),∴CB=9,CO=4=AB,
又∵CE=6,
∴E(6,4),BE=3,
∵∠B=90°,
∴Rt△ABE中,AE=
| AB2+BE2 |
∴△ABE的周长:3+4+5=12;
(2)①∵OP=1×t=t,
∴AP=9-t,
∵△PAE的面积等于△PCE的面积的一半,
∴当P在OA之间时,
根据
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(9-t)×4=6×4×
| 1 |
| 2 |
解得t=6;
当P在OA的延长线上时,
根据
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(t-9)×4=6×4×
| 1 |
| 2 |
解得t=12;
综上所述,当t为6或12秒时,△PAE的面积等于△PCE的面积的一半;
②如图,当∠PEA=90°时,△PAE为直角三角形,过点P作PF⊥BC于F,则

CF=OP=t,EF=6-t,BF=6-t+3=9-t=AP,
由勾股定理可得,PE2+AE2=AP2,
即(PF2+EF2)+AE2=AP2,
∴42+(6-t)2+52=(9-t)2,
解得t=
| 2 |
| 3 |
当∠EPA=90°时,△PAE为直角三角形,EP⊥OA,
此时,PE=OC=4,
∴Rt△APE中,AP=
| AE2-PE2 |
∴OP=9-3=6,
∴t=6;
∵EA与AP不垂直,
∴∠PAE不可能为直角;
综上所述,当t为6或
| 2 |
| 3 |
看了如图,长方形OABC的顶点A、...的网友还看了以下:
某乡镇企业2009年实际产值为10.6亿元,若上报为11.5亿元,则构成虚报统计资料的统计违法行为; 2020-05-21 …
已知某圆的方程是x的平方+y的平方=4,a、b为圆上两动点,m(1,1)为圆内一定点,若四边形ma 2020-06-03 …
[2009年苏州市初中结业考试]右图为反射弧的结构模式图.下列有关叙述中,不正确的是()A.若上图 2020-06-28 …
[2009年苏州市初中结业考试]右图为反射弧的结构模式图.下列有关叙述中,不正确的是()A.若上图 2020-06-28 …
如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC 2020-07-09 …
如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上 2020-07-21 …
如图,已知直线l与O相离,OA⊥l于点A,OA与O相交于点P,点B为O上一点,BP的延长线交直线l 2020-07-26 …
如图,在平面直角坐标系中,已知动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,OP 2020-07-30 …
如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB是⊙O上关于A 2020-07-31 …
常温下A.B两种无色气体组成的混合气体中只含N.H两种元素,且不论A.B以何种比例混合,两元素质量比 2020-11-05 …