早教吧作业答案频道 -->数学-->
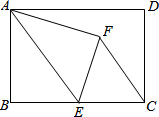
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=.
题目详情
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=___.

▼优质解答
答案和解析
过E作EH⊥CF于H,
由折叠的性质得: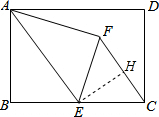 BE=EF,∠BEA=∠FEA,
BE=EF,∠BEA=∠FEA,
∵点E是BC的中点,
∴CE=BE,
∴EF=CE,
∴∠FEH=∠CEH,
∴∠AEB+∠CEH=90°,
在矩形ABCD中,
∵∠B=90°,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEH,∠B=∠EHC,
∴△ABE∽△EHC,
∴
=
,
∵AE=
=10,
∴EH=
,
∴sin∠ECF=sin∠ECH=
=
,
故答案为:
.
由折叠的性质得:
 BE=EF,∠BEA=∠FEA,
BE=EF,∠BEA=∠FEA,∵点E是BC的中点,
∴CE=BE,
∴EF=CE,
∴∠FEH=∠CEH,
∴∠AEB+∠CEH=90°,
在矩形ABCD中,
∵∠B=90°,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEH,∠B=∠EHC,
∴△ABE∽△EHC,
∴
| AB |
| EH |
| AE |
| CE |
∵AE=
| AB2+BE2 |
∴EH=
| 24 |
| 5 |
∴sin∠ECF=sin∠ECH=
| AB |
| AE |
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
看了如图,在矩形ABCD中,AB=...的网友还看了以下:
小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处 2020-04-27 …
二次函数Y=X^2-(M^2-4M+5/2)-2(M^2-4M+9/2)的图象与X轴的交点为A、B 2020-04-27 …
关于图中各点方向的判断,正确的是()A.b点在a点的东南方向B.c点在a点的西南方向C.d点在b点 2020-05-13 …
关于图中各点方向的判断,正确的是()A.b点在a点的东南方向B.c点在a点的西南方向C.d点在b点 2020-05-13 …
看图,回答3-5题关于图中各点方向的判断,正确的是()A.b点在a点的东南方向B.c点在a点的西南 2020-05-13 …
阅读如图,请选择6-8题.关于图中各点方向的判断,正确的是()A.b点在a点的东南方向B.c点在a 2020-05-13 …
关于图中各点方向的判断,正确的是()A.b点在a点的东南方向B.c点在a点的西南方向C.d点在b点 2020-05-13 …
阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点 2020-05-16 …
甲乙两人比赛折回跑,同时从A地出发,到达B地后,立刻返回,先回到A点的有获胜,甲先到B点在距B点2 2020-06-13 …
已知光线从点A(-3,4)射出,经x轴上的B点,在x轴反射,交y轴与C点,再经点C从y轴上反射恰经 2020-06-27 …