早教吧作业答案频道 -->数学-->
如图,在▱ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.(1)求证:△ABE≌△CDF;(2)若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.
题目详情
如图,在▱ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.
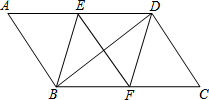
(1)求证:△ABE≌△CDF;
(2)若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.

(1)求证:△ABE≌△CDF;
(2)若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=CB,AD∥CB,∠A=∠C,∠ABC=∠ADC,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE=
∠ABC,∠CDF=
∠ADC,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA);
(2) 四边形EBFD是菱形;理由如下:
由(1)得:△ABE≌△CDF,
∴AE=CF,
∴DE=BF,
又∵DE∥BF,
∴四边形EBFD是平行四边形,
∵BD⊥EF,
∴四边形EBFD是菱形.
∴AB=CD,AD=CB,AD∥CB,∠A=∠C,∠ABC=∠ADC,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABE=∠CDF,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(ASA);
(2) 四边形EBFD是菱形;理由如下:
由(1)得:△ABE≌△CDF,
∴AE=CF,
∴DE=BF,
又∵DE∥BF,
∴四边形EBFD是平行四边形,
∵BD⊥EF,
∴四边形EBFD是菱形.
看了如图,在▱ABCD中,BE平分...的网友还看了以下:
在四边形ABCD中,∠A+∠C=180°,则∠B+∠D= 2020-05-01 …
在平行四边形ABCD中,若∠a=51°,则∠b=,∠c=,∠d= 2020-05-13 …
1.四边形的内角中最多有两个锐角.这句话怎么错了?2.若四边形ABCD的对角∠BAD与∠BCD的角 2020-05-21 …
如图1,若AB∥CD,则有∠B+∠D=∠E.(1)将点E移至图2的位置时,则∠B、∠D,∠E有什么 2020-06-12 …
把一根均匀电阻丝弯折成一个封闭的等边三角形ABC,如图所示.图中D为AB边的中点.如果A、C之间的 2020-07-01 …
给下面的题填空:如果a、b、c、d均为非零的自然数,则b\a*d\c=() 2020-07-04 …
填空题(只写答案)对于四边形ABCD,下面给出3个命题①若AB=BC,则CD=DA②若∠A=90° 2020-07-09 …
下列说法不正确的是A.若a,b,c,d成比例,则2a,2b,2c,2d也成比例.B.若a,b,c,d 2020-11-28 …
判断下列命题的真假已知a,b,c,d∈R(1)若ac>bc,则a>b(2)若a>-b,则c-ab>c 2020-12-13 …
设A.B.C.D为n阶方阵,E为n阶单位阵,则下列命题正确的是?(A)若A^2=0,则A=0(B)A 2021-01-12 …