早教吧作业答案频道 -->数学-->
已知正方形ABCD,点E、F分别在射线AB、射线BC上,AE=BF,DE与AF交于点O.(1)如图1,当点E、F分别在射向AB、BC上时,则线段DE于AF的数量关系是,位置关系是.(2)如图2,当点E在线段AB延
题目详情
已知正方形ABCD,点E、F分别在射线AB、射线BC上,AE=BF,DE与AF交于点O.
(1)如图1,当点E、F分别在射向AB、BC上时,则线段DE于AF的数量关系是___,位置关系是___.
(2)如图2,当点E在线段AB延长线上时,将线段AE沿AF进行平移至FG,连接DG.
①依题意将图2不全;
②小亮通过观察,实验提出猜想:在点E运动的过程中,始终有DG2=2AD2+2AE2.
小亮把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种方法:
想法1:连接EG,要证明DG2=2AD2+2AE2,只需证四边形FAEG是平行四边形及△DGE是等腰三角形.
想法2:延长AD、GF交于点H,要证明DG2=2AD2+2AE2,只需证△DGH是直角三角形.
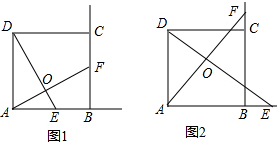
(1)如图1,当点E、F分别在射向AB、BC上时,则线段DE于AF的数量关系是___,位置关系是___.
(2)如图2,当点E在线段AB延长线上时,将线段AE沿AF进行平移至FG,连接DG.
①依题意将图2不全;
②小亮通过观察,实验提出猜想:在点E运动的过程中,始终有DG2=2AD2+2AE2.
小亮把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种方法:
想法1:连接EG,要证明DG2=2AD2+2AE2,只需证四边形FAEG是平行四边形及△DGE是等腰三角形.
想法2:延长AD、GF交于点H,要证明DG2=2AD2+2AE2,只需证△DGH是直角三角形.

▼优质解答
答案和解析
(1)∵四边形ABCD是正方形,
∴∠DAE=∠ABF=90°,DA=AB,
在△DAE和△ABF中,
,
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,即∠AOE=90°,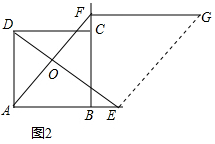
∴DE⊥AF,
故答案为:DE=AF;DE⊥AF;
(2)①补全图形如图所示:
②想法1::连接EG,如图2所示:
由题意得,AE=FG,AE∥FG,
∴四边形FAEG是平行四边形,
∴AF=EG,AF∥EG,
由勾股定理得,DE2=AD2+AE2,
在△DAE和△ABF中,
,
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∴DE=EG,
∵∠ADE+∠AED=90°,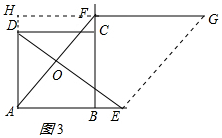
∴∠BAF+∠AED=90°,即∠AOE=90°,
∴DE⊥AF,
∴DE⊥EG,
∴DG2=2DE2,
∴DG2=2AD2+2AE2.
想法2:延长AD、GF交于点H,如图3所示:
由平移的性质得:AE=FG,AE∥FG,
∵AD⊥AB,
∴GH⊥AD,四边形CDHF是矩形,
∴∠H=90°,HF=DC=AD,
∴DG2=GH2+DH2,
∵HG=FG+HF,
∴HG=AE+HF=AE+AD,
同①得:BF=AH,
∵BF=AE,
∴HD=AE-AD,
∴DG2=(AE+AD)2+(AE-AD)2=2AD2+2AE2.
∴∠DAE=∠ABF=90°,DA=AB,
在△DAE和△ABF中,
|
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,即∠AOE=90°,

∴DE⊥AF,
故答案为:DE=AF;DE⊥AF;
(2)①补全图形如图所示:
②想法1::连接EG,如图2所示:
由题意得,AE=FG,AE∥FG,
∴四边形FAEG是平行四边形,
∴AF=EG,AF∥EG,
由勾股定理得,DE2=AD2+AE2,
在△DAE和△ABF中,
|
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∴DE=EG,
∵∠ADE+∠AED=90°,

∴∠BAF+∠AED=90°,即∠AOE=90°,
∴DE⊥AF,
∴DE⊥EG,
∴DG2=2DE2,
∴DG2=2AD2+2AE2.
想法2:延长AD、GF交于点H,如图3所示:
由平移的性质得:AE=FG,AE∥FG,
∵AD⊥AB,
∴GH⊥AD,四边形CDHF是矩形,
∴∠H=90°,HF=DC=AD,
∴DG2=GH2+DH2,
∵HG=FG+HF,
∴HG=AE+HF=AE+AD,
同①得:BF=AH,
∵BF=AE,
∴HD=AE-AD,
∴DG2=(AE+AD)2+(AE-AD)2=2AD2+2AE2.
看了已知正方形ABCD,点E、F分...的网友还看了以下:
E是平行四边形ABCD对角线交点,过点A,B,C,D,E分别向直线l引垂线,垂足分别为E是平行四边形 2020-03-31 …
主要的天线系列有哪些?(选择所有正确答案)A、全向天线B、单向天线C、定向天线D、八木天线A.B.C 2020-05-26 …
急性心肌梗塞最早期的心电图改变是( )A.ST段明显抬高,呈弓背向上的单向曲线B.出现异常Q波和ST 2020-06-07 …
平面电磁波的特性是电磁波是横波,E和B的传播方向是.E和B的方向互相.E×B沿波矢k的方向.E和B的 2020-11-02 …
线圈在水平放置的长直导线电流下方与导线在同一个平面内,做如图的运动:A向右平动,B向下平动,C绕轴转 2020-11-04 …
读图,(图中河谷流水自西向东流)分析判断下列各题:1.图中正确表示河谷发育位置的是()A.110°E 2020-12-08 …
读图(图中河谷流水自西向东流),图中正确表示河谷发育位置的是()A、110°E线B、30°N线C、a 2020-12-08 …
图为我国某地区等高线地形图(图中河水自东向西流),读图,回答以下问题。1.图中正确表示河谷发育位置的 2020-12-08 …
读图(图中河谷流水自西向东流),图中正确表示河谷发育位置的是()A.110°E线B.30°N线C.a 2020-12-08 …
读下图,(图中河谷流水自西向东流)分析判断下列各题小题1:图中正确表示河谷发育位置的是A.110°E 2020-12-27 …