早教吧作业答案频道 -->数学-->
如图,在正四棱锥P-AMDE,底面AMDE的边长为2,侧棱PA=5,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P-AMDE的外接球的
题目详情
如图,在正四棱锥P-AMDE,底面AMDE的边长为2,侧棱PA=
,B,C分别
为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.
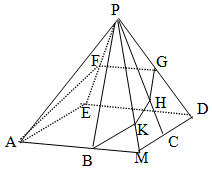
(1)求证:AB∥FG;
(2)求正四棱锥P-AMDE的外接球的表面积.
| 5 |
为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.

(1)求证:AB∥FG;
(2)求正四棱锥P-AMDE的外接球的表面积.
▼优质解答
答案和解析
(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.
又因为AB⊄平面PDE,DE⊂平面PDE
所以AB∥平面PDE.
因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,
所以AB∥FG.
(2) 连接AD,EM,相交于O′,易得AO′=
,PO′=
.
由正四棱锥P-AMDE的对称性,
得正四棱锥P-AMDE得外接球球心在线段PO′上,
不妨设为O点.设OA=OP=R,则OO′=
-R,
∵AO2=AO′2+OO′2,
∴R2=2+(
-R)2,
∴R=
∴S=4πR2=
,
∴正四棱锥P-AMDE的外接球的表面积为
.
又因为AB⊄平面PDE,DE⊂平面PDE
所以AB∥平面PDE.
因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,
所以AB∥FG.
(2) 连接AD,EM,相交于O′,易得AO′=
| 2 |
| 3 |
由正四棱锥P-AMDE的对称性,
得正四棱锥P-AMDE得外接球球心在线段PO′上,
不妨设为O点.设OA=OP=R,则OO′=
| 3 |
∵AO2=AO′2+OO′2,
∴R2=2+(
| 3 |
∴R=
5
| ||
| 6 |
∴S=4πR2=
| 25π |
| 3 |
∴正四棱锥P-AMDE的外接球的表面积为
| 25π |
| 3 |
看了如图,在正四棱锥P-AMDE,...的网友还看了以下:
A、B、C、D、E、F为短周期元素,非金属元素A最外层电子数与其周期数相同,B的最外层电子数是其所 2020-04-08 …
已知A、B、C、D、E、F是含有同一种元素的化合物,其中F是能使湿润红色石蕊试纸变蓝的气体,它们之 2020-05-02 …
如何解这类题已知A,B,C,D,E,F是含有同一种元素的化合物,其中F能使红色湿润石蕊试纸变蓝色, 2020-05-13 …
函数的概念问题高等数学里面,函数的定义是:设集数D包含于R,则称映射f:D→R为定义在D上的函数… 2020-06-08 …
设函数f(x)在x=0处连续,下列命题错误的是()A.若limx→0f(x)x存在,则f(0)=0 2020-06-12 …
readyfordry服装英语简写是R.F.D.,我同事说是readyfordry,但是我有点不理 2020-07-23 …
经济基础知识需求函数Qd=f(p)中的f代表的对应法则是什么?如果f的对应法则为,价格之外的其他因 2020-08-02 …
在Rt△ABC中,∠ACB=90°,tan∠BAC=12,点D在边AC上(不与A、C重合),连结BD 2020-11-01 …
A、B、D、E、F为短周期元素.非金属元素A最外层电子数与其周期数相同,B的最外层电子数是其所在周期 2020-12-07 …
在一个4变量逻辑函数F(A,B,C,D)中,子项AD意味着包含了的多少个最小项在一个4变量逻辑函数F 2020-12-08 …