早教吧作业答案频道 -->数学-->
问题背景甲、乙、丙三名同学探索课本上一道题:如图1,E是边长为a的正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.任务要求:(1)请你在图1
题目详情
问题背景
甲、乙、丙三名同学探索课本上一道题:如图1,E是边长为a的正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
任务要求:
(1)请你在图1中画出旋转后的图形
甲、乙、丙三名同学又继续探索:
在正方形ABCD中,∠EAF=45°,点F为BC上一点,点E为DC上一点,∠EAF的两边AE、AF分别与直线BD交于点M、N.连接EF
甲发现:线段BF,EF,DE之间存在着关系式EF=BF+DE;
乙发现:△CEF的周长是一个恒定不变的值;
丙发现:线段BN,MN,DM之间存在着关系式BN2+DM2=MN2
(2)现请你参与三位同学的研究工作中来,你认为三名同学中哪个的发现是正确的,并说明你的理由.
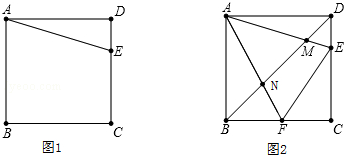
甲、乙、丙三名同学探索课本上一道题:如图1,E是边长为a的正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
任务要求:
(1)请你在图1中画出旋转后的图形
甲、乙、丙三名同学又继续探索:
在正方形ABCD中,∠EAF=45°,点F为BC上一点,点E为DC上一点,∠EAF的两边AE、AF分别与直线BD交于点M、N.连接EF
甲发现:线段BF,EF,DE之间存在着关系式EF=BF+DE;
乙发现:△CEF的周长是一个恒定不变的值;
丙发现:线段BN,MN,DM之间存在着关系式BN2+DM2=MN2
(2)现请你参与三位同学的研究工作中来,你认为三名同学中哪个的发现是正确的,并说明你的理由.

▼优质解答
答案和解析
(1)画图如图1所示;(2)甲、乙、丙三名同学的发现都是正确的;①甲发现正确;理由如下:如图2所示,延长CB到K,使BK=DE,连AK,∵四边形ABCD是正方形,∴AB=AD,∠ABF=∠ABK=∠ADE=90°,在△AKB和△AED中,AD=AB...
看了问题背景甲、乙、丙三名同学探索...的网友还看了以下:
如图所示,一质量为m,电量为q的带电粒子从静止出发被电压为U的电厂加速,然后垂直进入另一个电厂强度 2020-04-26 …
如图所示,电子从电子枪发出(初速度可不计)后经加速电场加速,从两偏转极板的正中间进入偏转电场.已知 2020-05-17 …
电子从静止出发被u的电压加速、沿着与电场垂直的方向进入另一个电场强度为e的匀强偏转电场、进入方向与 2020-06-06 …
如图,在Rt△ABC中,∠C=90°,AC=BC,将其绕点A逆时针旋转15°得到Rt△AB′C′, 2020-07-13 …
已知在△ABC中,∠ACB=90°,AB=10,cosA=35(如图),将△ABC绕着点C旋转,点 2020-07-21 …
如图,△AOB中,∠AOB=90°,AO=2,BO=4,△AOB绕顶点O逆时针旋转到△A′OB′处 2020-07-24 …
九年级上册——旋转如图,△ABC中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O顺时针旋转 2020-11-03 …
如图所示,初速度为零的电子(电荷量为e、质量为m),经电压为U1的加速电场加速后从金属板的小孔穿出, 2021-01-02 …
如图所示,一质量为m,电量为q的带电粒子从静止出发被电压为U的电场加速,然后垂直进入另一电场强度为E 2021-01-02 …
如图所示,喷墨打印机中的墨滴在进入偏转电场之前会被带上一定量的电荷,在电场的作用下使电荷发生偏转到达 2021-01-02 …