早教吧作业答案频道 -->数学-->
在正方形ABCD的外侧作直线AP,过点B作BO⊥AP,垂足为O.(1)在图中画出△ABO关于直线AP对称的△AEO;(2)在(1)的条件下,连结DE.①当∠PAB=20°时,求∠ADE的度数;②当∠PAB=α,且0°<α
题目详情
在正方形ABCD的外侧作直线AP,过点B作BO⊥AP,垂足为O.
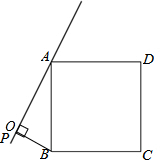
(1)在图中画出△ABO关于直线AP对称的△AEO;
(2)在(1)的条件下,连结DE.
①当∠PAB=20°时,求∠ADE的度数;
②当∠PAB=α,且0°<α<90°(α≠45°)时,直接写出△ADE中∠ADE的度数(结果可用含α的代数式表示).

(1)在图中画出△ABO关于直线AP对称的△AEO;
(2)在(1)的条件下,连结DE.
①当∠PAB=20°时,求∠ADE的度数;
②当∠PAB=α,且0°<α<90°(α≠45°)时,直接写出△ADE中∠ADE的度数(结果可用含α的代数式表示).
▼优质解答
答案和解析
(1)如图1所示:
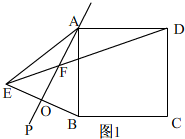
(2)①由对称得∠PAB=∠PAE=20°,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=20°,
∴∠EAD=130°,
∴∠ADE=
=25°;
②Ⅰ、当0°<α<45°时,如图1,由对称得∠PAB=∠PAE=α,AE=AB=AD,
∴∠BAE=2∠PAB=2α,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=∠BAD+∠BAE=∠BAD+2∠BAP=90°+2α,
∵AE=AB,
∴∠ADE=
(180°-∠DAE)=
[180°-(90°+2α)]=45°-α;
Ⅱ、当45°<α<90°时,如图2,
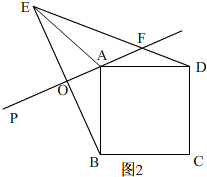
由对称得∠PAB=∠PAE=α,AE=AB=AD,
∴∠BAE=2∠PAB=2α
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=360°-∠BAD-2∠BAP=360°-90°-2α=270°-2α,
∵AE=AB,
∴∠ADE=
(180°-∠DAE)=
[180°-(270°-2α)]=α-45°.
∴当0°<α<45°时,∠ADE=45°-α,当45°<α<90°时,∠ADE=α-45°.

(2)①由对称得∠PAB=∠PAE=20°,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=20°,
∴∠EAD=130°,
∴∠ADE=
| 180°-130° |
| 2 |
②Ⅰ、当0°<α<45°时,如图1,由对称得∠PAB=∠PAE=α,AE=AB=AD,
∴∠BAE=2∠PAB=2α,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=∠BAD+∠BAE=∠BAD+2∠BAP=90°+2α,
∵AE=AB,
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
Ⅱ、当45°<α<90°时,如图2,

由对称得∠PAB=∠PAE=α,AE=AB=AD,
∴∠BAE=2∠PAB=2α
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=360°-∠BAD-2∠BAP=360°-90°-2α=270°-2α,
∵AE=AB,
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴当0°<α<45°时,∠ADE=45°-α,当45°<α<90°时,∠ADE=α-45°.
看了在正方形ABCD的外侧作直线A...的网友还看了以下:
P(A/B)+P(A非/B非)=1证明AB独立我这样证:原始=P(A/B)+1-P(A/B非)=1 2020-04-06 …
计算题(P/A,10%,4)=3.1699(P/F,10%,1)=0.9091(P/A,10%,5 2020-04-07 …
概率题急求解1设A,B为随机事件且P(A)=0.7,P(A-B)=0.3,求P(A非B非).2设A 2020-04-12 …
设S=|a1,a2,...,an|是整数集,其中n>1.对于S的非空子集A,定义P(A)为A的一切 2020-04-26 …
设S=|a1,a2,...,an|是整数集,其中n>1.对于S的非空子集A,定义P(A)为A的一切 2020-04-26 …
一道高2化学平衡题在线等哦~一定体积2A=B+XC温度不变,平衡后,体积增大P%,A的转化率也为P 2020-04-27 …
设S=|a1,a2,...,an|是整数集,其中n>1.对于S的非空子集A,定义P(A)为A的一切 2020-05-16 …
设A,B是两个互斥事件,它们都不发生的概率为0.4,且P(A)=2P(B),则P(A的互斥事件)= 2020-05-16 …
在海上运输货物保险基本险的保险责任中,平安险(F.P.A)的英文基本含义是( )。 2020-05-22 …
概率题,设p(A)=x,p(B)=y且p(A交B)=z,求p(A的逆交B). 2020-05-23 …