早教吧作业答案频道 -->数学-->
如图,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-9x+18=0的两根(OA>OC),BE=5,tan∠ABO=34(1)求点A,C的坐标;
题目详情
如图,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-9x+18=0的两根(OA>OC),BE=5,tan∠ABO=
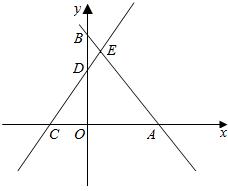
(1)求点A,C的坐标;
(2)求AB的长;
(3)若反比例函数y=
的图象经过点E,求k的值.
| 3 |
| 4 |

(1)求点A,C的坐标;
(2)求AB的长;
(3)若反比例函数y=
| k |
| x |
▼优质解答
答案和解析
(1)方程x2-9x+18=0,
变形得:(x-3)(x-6)=0,
解得:x=3或x=6,
∴OA=6,OC=3,
则A(6,0),C(-3,0);
(2)∵在Rt△AOB中,tan∠ABO=
,
∴
=
,
∴OB=8,
根据勾股定理得:AB=
=10;
(3)过E作EF⊥x轴,交x轴于点F,
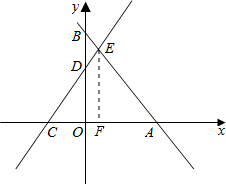 ∵∠EAF=∠BAO,∠EFA=∠BOA=90°,
∵∠EAF=∠BAO,∠EFA=∠BOA=90°,
∴△AEF∽△ABO,
∵OB=8,AB=10,AE=AB-BE=10-5=5,
∴
=
,即
=
,
∴EF=4,即E纵坐标为4,
设直线AB解析式为y=mx+n,
把A(6,0),B(0,8)代入得:
,
解得:
,
∴直线AB解析式为y=-
x+8,
把y=4代入得:x=3,即E(3,4),
把E坐标代入反比例解析式得:k=12,
则k的值为12.
变形得:(x-3)(x-6)=0,
解得:x=3或x=6,
∴OA=6,OC=3,
则A(6,0),C(-3,0);
(2)∵在Rt△AOB中,tan∠ABO=
| 3 |
| 4 |
∴
| OA |
| OB |
| 3 |
| 4 |
∴OB=8,
根据勾股定理得:AB=
| OA2+OB2 |
(3)过E作EF⊥x轴,交x轴于点F,
 ∵∠EAF=∠BAO,∠EFA=∠BOA=90°,
∵∠EAF=∠BAO,∠EFA=∠BOA=90°,∴△AEF∽△ABO,
∵OB=8,AB=10,AE=AB-BE=10-5=5,
∴
| EF |
| OB |
| AE |
| AB |
| EF |
| 8 |
| 5 |
| 10 |
∴EF=4,即E纵坐标为4,
设直线AB解析式为y=mx+n,
把A(6,0),B(0,8)代入得:
|
解得:
|
∴直线AB解析式为y=-
| 4 |
| 3 |
把y=4代入得:x=3,即E(3,4),
把E坐标代入反比例解析式得:k=12,
则k的值为12.
看了如图,直线AB与x轴、y轴分别...的网友还看了以下:
如图,OP是一条射线,OA,OB,OC是三条线段,其中OA=a,OB=b,OC=c,并且∠BOP= 2020-05-16 …
直角梯形OABC中,点A,C分别在x轴,y轴的正半轴上,OA∥BC,OA=6,AB=5,BC=2, 2020-05-16 …
在平面直角坐标系中,矩形OABC的顶点O在坐标原点上,顶点A,B分别在x轴,y轴的正半轴上,OA= 2020-05-17 …
在射线OA上取一点A,使OA=4,以点A为圆心做一个直径为4cm的远,现有一条以点O为端点的射线O 2020-05-23 …
四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是()A.OA=OB=OC= 2020-06-13 …
如图,在平面直角坐标系中,直线AB分别与X轴正半轴、Y轴正半轴交于点A、B,OA=3,OB=根号3 2020-06-27 …
如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌ 2020-07-10 …
已知椭圆的中心是O,长轴.短轴的长分别为2a,2b(a大于b大于0),A,B分别为椭圆上的两点,而 2020-07-31 …
四边形周长最短在坐标系中,矩形OACB的顶点O的原点,顶点A,B分别在x轴,y轴的真半轴上,OA=3 2020-11-24 …
如图所示,杠杆AOB的两端分别挂着重为GA和GB的两个物体,杠杆平衡时AO处于水平位置,若GA=GB 2020-12-02 …